分散(Variance) 階級の代表値を変数として、先ず平均を求め、次に変数と平均の差 (偏差)の2乗を作り、それに度数を掛けて合算し、度数の合計で割って求めます。 あるいは変数の2乗に度数を掛けて合算し、度数の合計で割って変数の2乗平 均を求め、これから平均の2乗を引いても、同じ結果となります。どちらの方法 でも構いません。
変数が階級に区分されていないときや、階級に区分されていても階級に幅が ないときは、その変数で計算します。
標準偏差(Standard deviation) 分散の平方根(正の方)です。
変動係数(Coefficient of variation, Relative standard deviation) 標準偏差を 平均で割って求めます。変動係数は相対標準偏差ともいいます。
 計算例(1) 次表は、ある果樹園から1季節に出荷された桃の
重さ(g)の分布です。(階級は、以上-未満)
計算例(1) 次表は、ある果樹園から1季節に出荷された桃の
重さ(g)の分布です。(階級は、以上-未満)階級① 中央値② 個数③ 重さの計④ 160 -170 165 93 15454 170 -180 175 165 28658 180 -190 185 252 45986 190 -200 195 318 63003 200 -210 205 355 73100 210 -220 215 293 63019 220 -230 225 176 38932 230 -240 235 132 31120 240 -250 245 84 20298 ---------------------------------------- 計 -
階級の重さの計を用いた場合、桃の重さの分散は、関連ページにより平均が 203.19593であったので 変数をそのまま2乗する方法をとれば、 {(93*166.172042+165*1173.684852+252*182.484132+318*198.122642+ 355*205.915492+293*215.081912+176*221.204552+132*235.757582+ 84*241.642862}/1868-203.195932=402.9372(g2)
標準偏差は √402.9372=20.0733(g)
変動係数は 20.0733/203.19593=0.09879
となります。
階級の中央値を用いた場合 {(93*(165-203.32976)2+165*(175-203.32976)2+252*(185-203.32976)2+ 318*(195-203.32976)2+355*(205-203.32976)2+293*(215-203.32976)2+ 176*(225-203.32976)2+132*(235-203.32976)2+84*(245-203.32976)2}/ 1868=416.2681(g2)
標準偏差は √416.2681=20.4027(g)
変動係数は 20.4027/203.3298=0.10034
となります。
関連応用問題
 計算例(2) F氏宅の60日間の電話の呼数の分布が、次表の通りのとき、
呼数の分散を求めるには、呼数の2乗に日数を掛けて合算し、日数の
合計で割り、別に求めた平均の2乗を引いて求めます。
計算例(2) F氏宅の60日間の電話の呼数の分布が、次表の通りのとき、
呼数の分散を求めるには、呼数の2乗に日数を掛けて合算し、日数の
合計で割り、別に求めた平均の2乗を引いて求めます。1日の呼数 X 日数 f 0 5 1 8 2 10 3 12 4 9 5 7 6 4 7 3 8 1 9 1 ------------------- 計 60
呼数の2乗平均は
(0*0*5+1*1*8+2*2*10+3*3*12+4*4*9+5*5*7+6*6*4 +7*7*3+8*8*1+9*9*1)/(5+8+10+12+9+7+4+3+1+1) =15.1833
平均(関連ページ)の2乗は 3.28332=10.7803ですから
分散は
=15.1833-10.7803=4.4031(呼2)
となります。
標準偏差は √4.4031=2.0983(呼)
変動係数は 2.0983/3.2833=0.6391
です。
----------------
 理論
理論K個のデータ Xi (幅のある階級に区分されているときは、その中央値 など)とそれぞれに対応する度数 fi が
X1,X2,....,XK f1,f2,....,fK
であるとき、X の分散は
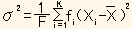 (1)
(Fは各 fiの合計)
(1)
(Fは各 fiの合計)と表わし、これを分散といいます。この式は
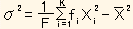 =(ΣfX2)/F-{(ΣfX)/F}2 (2)
=(ΣfX2)/F-{(ΣfX)/F}2 (2)と変形できます。式 (1),(2)は数理的に同じで、どちらを使っても構い ません。実務では (2)式がよく用いられます。
標準偏差は
σ=√(σ2)
変動係数は
CV=σ/
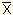
です。 -------------------
| 分散などの意味と計算手順のまとめ
意味:分散は散布度(2次)の基本的尺度、主に理論で使用。 |
 練習問題(1)
練習問題(1)G氏の週ごとの晩酌の頻度は下表の通りです。 晩酌の回数の分散などを求めなさい。
回数 X 週の数 f 0 1 1 5 2 7 3 14 4 13 5 8 6 3 7 1 ---------------- 計 52
[答(計算値) 分散 2.2056(回2)、標準偏差 1.4851(回)、変動係数 0.4339]
練習問題(1)の関連ページ
 練習問題(2)
練習問題(2)ある村に、次のような世帯統計があります。 世帯人員の分散などを求めなさい。
世帯人員規模 世帯数 世帯人員 1 52 52 2 449 898 3 1048 3144 4 926 3704 5 530 2650 6-7 270 1728 8-10 24 205 11以上 1 12
[答(計算値)分散 1.7451(人2),標準偏差 1.3210(人),変動係数 0.3518]
(この問題では、世帯人員規模6人以上の階級の代表値は、世帯数と 世帯人員から割り戻す)
練習問題(2)の関連ページ




















