(階級に幅がある場合)
変数が階級に区分され、階級ごとの度数が示されているときは、 変数の平均は通常、階級の代表値とそれに対応する度数を用いて 求めます。すなわち、階級の代表値に度数を掛けて合算し、度数の 合計で割って求めます。
階級の代表値が不明で、階級の代表値が必要のときは、階級の中 央値などを階級の代表値とします。階級の変数の総和が示されてい るときは、階級の代表値を割り出すことができます。
 計算例 次表は、ある果樹園から1季節に出荷された桃の
重さ(g)の分布です。(階級は、以上-未満)
計算例 次表は、ある果樹園から1季節に出荷された桃の
重さ(g)の分布です。(階級は、以上-未満)階級① 中央値② 個数③ 重さの計④ 160 -170 165 93 15454 170 -180 175 165 28658 180 -190 185 252 45986 190 -200 195 318 63003 200 -210 205 355 73100 210 -220 215 293 63019 220 -230 225 176 38932 230 -240 235 132 31120 240 -250 245 84 20298 ---------------------------------------- 各階級の重さの計を用いた場合、桃1個当たりの平均の重さは、 (15454+28658+45986+63003+73100+63019+38932+31120+20298)/ (93+165+252+318+355+293+176+132+84) =379570/1868 =203.19593 =203(g) 各階級の中央値を用いた場合、 (65*93+175*165+185*252+195*318+205*355+ 215*293+225*176+235*132+245*84)/(93+165 +252+318+355+293+176+132+84) =379820/1868 =203.32976 =203(g)
となります。 ------------------------------
 理論
理論度数分布表の階級の代表値 X と度数 f が、
階級 代表値 X 度数 f . X1 f1 . X2 f2 省 . . 略 . . . . . . XK fK
のとき、X の平均は
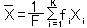 (a)
(Fは各 fiの合計)
(a)
(Fは各 fiの合計)となります。 -------------------------------
| 意味と計算手順のまとめ 意味:集団の基本的代表値の一種
計算手順:1、幅のある階級に代表値を立てる。 |
 練習問題
練習問題ある村に、次のような世帯統計があります。 1世帯当たりの世帯人員を求めなさい。
世帯人員規模 世帯数 世帯人員 1 52 52 2 449 898 3 1048 3144 4 926 3704 5 530 2650 6-7 270 1728 8-10 24 205 11以上 1 12
[答 3.8人 (計算値 3.755'4')]
(この問題では、世帯人員規模6人以上の部分に注意します。 階級と、階級の代表値は平均の計算には必要ありませんが、 分散などの計算には必要です。)




















