(階級に幅がない場合)
度数分布の算術平均は、変数の、度数を重み(ウエイト)とした加重算術平均です。 変数に度数を掛けて合算し、度数の合計で割って求めます。
 計算例 F氏宅の60日間の電話の呼数の分布が、次表の通りのとき、
1日当たりの平均呼数を求めるには、呼数と日数を掛けて合算し、日数の
合計で割ります。
計算例 F氏宅の60日間の電話の呼数の分布が、次表の通りのとき、
1日当たりの平均呼数を求めるには、呼数と日数を掛けて合算し、日数の
合計で割ります。1日の呼数 X 日数 f 0 5 1 8 2 10 3 12 4 9 5 7 6 4 7 3 8 1 9 1 ------------------- 計 60
1日当たりの平均は
(0*5+1*8+2*10+3*12+4*9+5*7+6*4+7*3+8*1+9*1)/(5+ 8+10+12+9+7+4+3+1+1) =197/60 =3.28333 =3.28(呼)
となります。 -----------
 理論
理論K個のデータ X と、それぞれに対応する度数 f が
X1,X2,....,XK f1,f2,....,fK
であるとき、X の平均は
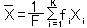 (a)
(Fは各 fiの合計)
(a)
(Fは各 fiの合計)となります。 度数は、重みの一種で、整数です。(相対度数や一般ウエイトは小数をとります。) -----------
| 意味と計算手順のまとめ 意味:集団の基本的代表値の一種
計算手順:1、データから K, F, ΣfX を求める。 |
 練習問題
練習問題G氏の週ごとの晩酌の頻度は下表の通りです。 晩酌の週平均回数を求めなさい。
回数 X 週の数 f 0 1 1 5 2 7 3 14 4 13 5 8 6 3 7 1 ---------------- 計 52 [答 3.4(回) (計算値 3.423)]
変数が階級に分けられているときは、度数に掛けるのは階級の代表値 になります。
階級の代表値が示されていなくて、階級の代表値が必要のときは、階級 の中央値などを階級の代表値とします。
階級の代表値が示されていなくても、変数の延べの値(変数の元の値と 度数との積)が示されているときは、それを用いて平均を計算すること ができます。




















