Calculation form 1 for t-distribution. Dr.Funatsu, Professor of Meisei university, Tokyo.　Mail　Contents of forms　Top page

...

[Input] Degree of freedom n=
Input as a≦b. If input b＜a, the value of a and b are exchanged.
E is an index of calculation errors and
0.00001≦E≦0.01
a= b=
E=

[Output]
Value for calculation a=
Value for calculation b=
Probability density(a)=
Probability density(b)=
Mean of t= (n≧2)
Variance of t= (n≧3)


Area of t≦a(probability A)=
Area of a＜t≦b(probability B)=
Area of b＜t(probability C)=
Total area(A+B+C)=1

Positions of a and b are fixed in the image below, irrespective of input values
in the left column.

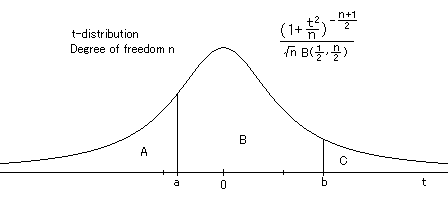
.........................................................................To seek b for given C.

Referring values of gamma- and beta-function. n=（possible errors in
decimals of lower position）
　Γ(n/2)= , Γ(n/2+0.5)= , Β(0.5, n/2)=

When n is large, values may be shown in index style as 3.14e+20. Be careful of
last place of decimals.


Comparison of calculated values for area 0-b of the distribution. Values for E=0.001 have better
precision than those for E=0.01.
 
Degree of freedom n=1 
          b=1      b=2      b=5      b=10      b=30      b=50
E=0.01    0.2492   0.3520   0.4372   0.46829   0.48939   0.49363
E=0.001   0.2499   0.3524   0.4371   0.46827   0.48939   0.49363

Degree of freedom n=5 
          b=1       b=2       b=3       b=4       b=5        
E=0.01    0.317     0.448     0.485     0.49486   0.49795
E=0.001   0.318     0.449     0.484     0.49484   0.49794
 
Degree of freedom n=20 
          b=1       b=2       b=3       b=4       b=5        
E=0.01    0.334     0.4700    0.4965    0.49965   0.49996
E=0.001   0.335     0.4703    0.4964    0.49964   0.49996