バグダッドの衰退
最初の三人のカリフの黄金時代後２世紀の間、バグダッドは、学問活動の中心であり続けた。マームーンの死(833年)後、政治的覇権は失われ始めた事実はあるが。しかし、1000年までに、その都の精神的覇権は過ぎ去り、西方アラビアの知の地位が、メソポタミアのカリフたちの都にとって代わられ始めた。不寛容なタタール族であるセルジュク・トルコが、以前はカリフたちにうまく支配されていた多くの地域を侵略し荒廃させ、パレスチナの聖都を攻略し、彼らの冷酷な行動は、十字軍のための口実を与えた。1258年、モンゴル人たちがバグダッドを奪取し、その時以降、そこはほとんど名前だけのものとなった。残忍な力が、東イスラム帝国でかくまで注目を引いた理想主義を終わらせた。
カリフの都で、数学に真に貢献した最後の人達の中に、アル・カルキ(al-Karkhi)(1)がいた。彼は、1029年頃に没している。彼の知られざる最初の著作は、算術(Kafi fil Hisab)(2)、恐らく、1010年頃と1016年との間に書かれたもので、もっぱらというわけではないにしても、ヒンドゥーの資料から広く取られている。(3)それには、当時の多くの著述家によって提示された算術の要素を含んでいるだけでなく、the rules of quarter square も含んでいる。
( a+b /2 )^2 - ( a-b /2)^2 = ab
恐らく、ヒンドゥーに起源のある公式だろう。また、次のような公式で示される乗法の方式も与えている。
( 10a + a )( 10b + b ) = [ ( 10a + a )b + ab ]*10 + ab
と
( 10a + b )( 10a + c ) = ( 10a + b + c )*a*10 + bc
平方根の近似を求めるには、アル・カルキは、他にもいろいろある中で、次のようにしている。
m = aa + r では、√m = a + r/(2a+1)
ｒ <= a のとき、√m = a + r/2a
彼は、また、平面図形の計算、特に無理数を扱うようなものについて考えており、ヘロンの公式√s(s-a)(s-b)(s-c)を含んでいる。
その著作は、最後に代数を扱い、二次方程式と第２巻で議論されたアル・ジャブル(al-jabr)とアル・ムカバラ(al-muqubala)という一般的なアラビア語の説明を含んでいる。
しかし、アル・カルキは、彼の代数「ファクリ(Fakhri)」(4)で最もよく知られている。それは、代数的量、（平方）根、一次と二次の方程式、不定解析(indeterminate analysis)や問題の解法の一般的な操作を含んでいる。二次方程式は、xxxx+5xx=126のような形式を含んでおり、全般に二次方程式の解法は、方程式
axx+bx=c
と定式
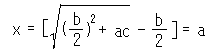
と表される公式によっている。
その公式は、初期のアラビアの著作においてのように、幾何学的に説明されている。彼によって与えられた様々な問題は、明らかにアル・フワーリズミーやディオファントゥスによって示唆されているもので、
xxx + yyy = zz,
xx - yy = zzz,
xxyyy = zz,
と xxx + 10xx = yy
の積分的解法(integral solution)の発見や
xx - yyy = zz
と xxx + yy = zzz,
の分数的解法(fractional solution)の発見のような場合も含んでいる。
その著作は、アラビア人の最も学問的な代数として位置づけられている。
１１世紀のマイナーな著述家たちの中で、次の人達は、簡単に言及しておく価値がある。
モハメド・イブン（ビン）・アル・レイト(Mohammed ibn al-Leit)(5)は、1000年頃生きていて、（角の）三分割の問題(trisection)に興味を持ち、正七角形や正九角形の作図について書いている。
ハミド・イブン（ビン）・アル・キディル(Hamid ibn al-Khidir)(6)は、アストロラーベについて著述し、方程式の xxx + yyy = zzz は、解けないと主張した。
マンスール・イブン（ビン）・アリ(Mansur ibn 'Ali)(7)は、天文学の器具や三角法、球面正弦？(spherical sines)やプトレマイオスの「アルマゲスト」について著述した。
アル・ナサヴィ(Al-Nasavi)は、ヒンドゥーの算術とアルキメデスの著作について書いている。(8)
１１世紀初め、当時の数学史に関する最も優れた著述家の一人は、アルベルニ(Alberuni)(9)であった。彼は、ムナジミン(munajjimin)、すなわちアラビア人の占星術師-天文学者の一人であった。彼は、インドを訪れ、その国とその国の数学その他の学問の著作を丹念に研究した。彼は、当時の知識が低下した状態を次のような言葉で要約している。「私たちが学問について知っていることは、過ぎ去ったよき時代のわずかな遺物にすぎない。」晩年に、彼はインドについて著作を書き、中世が生み出したヒンドゥー数学の最も優れた要約を、私たちはこの著作に負っている。
アルベルニの同時代の人の中に、キリスト教ヨーロッパでは、アヴィケンナ(Avicenna)(980-1037)(10)として知られる有名な医学者で哲学者である人がいた。彼は、ボカラ(Bokhara)から遠くないカルミタン(Kharmitan)近くのサファル(Safar)で生まれた。彼は、アリストテレス、ユークリッド（エウクレイデス）、天文学、音楽、医学と算術について著述し、彼の数の扱いはギリシアのモデルに基づいている。
イブン（ビン）・アル・シャラー（アッシャラー）(11)は、1153/54年に没した人だが、彼は、バグダッドをかくも有名にしたペルシアの学者たちの後の世代の一人であった。東方の多くの数学者と同様、彼は、また哲学と医学をも修めた。--後者（医学）は、一部、癒しの芸術と占星術との想像上の関係のためであったが。彼は、バグダッドに生まれ、最後には、ダマスカスへ行って、そこで没した。彼は、幾何学について著述し、彼の著作の写本は、明らかに断片的だが、今日も現存している。
１２世紀は、古代アラビアの学問の中心地においての数学には、それほど注意を向けず、ペルシアの学問（科学）に多くの注意を向ける。ペルシアの数学と文学に輝きを加えた人々の名の中で、最も優れているのは、イギリスの作家たちには、一般にオマール・クワィヤム(Omar Khayyam)(1100年頃)(12)として知られる詩人である。彼は、主として、「ルバイヤート(Rubaiyat)」(13)の著者として西欧世界に知られているが、ユークリッドや天文学についても著作しており(14)、代数については、価値ある論文で貢献した。(15)
オマール・クワィヤムの少し後、コラサン(Khorasan)生まれのもう一人のペルシア人が、その名を偉大にしている。この著述家は、アル・ラツィ(al-Razi)といい(16)、ペルシアの指導的哲学者、医師、そして数学者として知られている。彼の数学への貢献は、主として幾何学の分野においてであった。
１２世紀のアラビアの学者たちの中で、最もよく知られた一人が、ケマル・エッディン・イブン（ビン）・コニス(Kemal ed-din ibn Yunis)、すなわちイブン（ビン）・マナ(ibn Mana)(17)であった。彼は、チグリス川沿いのモスル(Mosul)で生まれた。彼の数の理論と円錐曲線に関する著作は、アラビアの同時代の人々に高く評価された。
最後に名の挙げられた著述家と同時代に、タアシフ(Taasif)(18)、上エジプトの生まれてで、法学者、技術者そして数学者であった人がいた。彼は、ユークリッド（エウクレイデス）の公準・公理について書くことで、数学の基礎に関心のあったことを示している。
１１−１２世紀において、セルジュク・トルコが不寛容であって、知的生活を送ることを困難にしていたというなら、1206年と1227年との間のチンギス・カーンによって導かれた大モンゴルの襲来は、そうした生活を不可能なものにした。彼の征服、そして彼の息子による征服は、中国北部からトルキスタンやペルシアを通ってインダス川のほとりに至るまで、文明社会のかなりの部分を含んでいた。息子のオゴタイ(Oktai)(1241年没)は、父親同様、極めて残忍で、ヨーロッパのほとんど半分を略奪し、征服全体の結果、かつて中央アジアや西アジアの栄光であったすべての知的中心を不毛の地とした。確かに、これらの暴君の後継者のうち、フビライ・ハン(1216-1294年)とチムール、すなわち、タメルラン(Tamerlane)(1336-1405年)は、よりよい生活のために貢献したが、２世紀に及ぶモンゴルの侵入の記録は、歴史すべての中で最も暗いものの一つである。
１３世紀には、ペルシアの一人の著述家だけが特別に名を挙げるに値する。そして、彼は、晩年をバグダッドで過ごしてさえいた。この著述家は、ナシル・エッディン（Nasir ed-din)(19)といい、コラサン(Khorasan)のトゥス(Tus)の生まれである。彼はオールラウンドな学者であって、三角法、天文学、計算法、幾何学そしてアストロラーベの制作と使用について著述している。
アラビアの著述家では、イブン（ビン）・アル・ヤシミン(Ibn al-Yasimin)(20)というモロッコに住んでいた人が、主として、彼が代数について書いた詩、アルジュザ(Arjuza)の影響のために知られている。いくつかの写本が、まだ存在し、それは、カルメン・デ・アルゴリズモ(p.226)がアルゴリズムに関して持っていたように、代数を広めるのに何らかの影響を及ぼしたように思える。ハレブ(Haleb)（アレッポ(Aleppo)）生まれのイブン（ビン）・アル・ルブディ(Ibn al-Lubudi)(21)は、その世紀、算術、代数そしてエウクレイデス（ユークリッド）の著作で知られていた。しかし、アラビアの学問に関する関心は急速に低下しつつあり、他には唯一人の名だけが、１３世紀の記録では言及に値するに過ぎない。それは、アル・トゥシ(al-Tusi)(22)という、トゥス(Tus)生まれのもう一人の優れた人物である。彼は、幾何学と代数について著述し、「トゥシの棒(Tusi's staff)」として知られるアストロラーベの一つの形を発明した。イスラムは、数学に関して支配力を失っていた。数学世界は、中国に一つの中心、そしてキリスト教ヨーロッパにもう一つの中心がある双曲線になりつつあって、その分岐点には何もなかった。
この時期、近東で最も名のあるキリスト教著述家は、バル・ヘブラエウス(Bar Hebraeus)(23)という人で、彼の父親はアーロンという名のユダヤ人でキリスト教会に入った人であった。息子が２０才になった時(1246年)、彼は、マラティア(Malatia)近くのグボス(Gubos)のヤコブ（教会）の司教(Jacobean bishop)にならされ、後に、他の教会の重要な地位に就いている。彼は、天文学について著述し、エウクレイデス（ユークリッド）とプトレマイオスについて講義した。(24)
１４世紀には、かなりの優れたイスラム教徒として、三人だけが世界の数学者の中に入れられようが、その一人として天才ではなかった。少なくとも、その時代、二人がエジプトに住んでいた。算術についての著述家イブン（ビン）・アル・ハイム(Ibn al-Ha'im)(25)と天文学、三角法、算術、暦、数学の表について著述したイブン（ビン）・アル・メジディ(Ibn al-Mejdi)(26)が。その時代の第三のアラビアの著述家は、一般に、イブン・アル・シャティル(Ibn al-Shatir)(27)として知られるひとで、三角法、アストロラーベと天文学についての著作を残し、少し数学表を作成している。
１５世紀に生きていた数学に関心のあったアラビア・ペルシアの代表者の中で、唯一何らかの天才を保持していたように思える人は、ウルグ・ベク(Ulugh Beg)(1393-1449)(28)であったが、この天才でさえ、並はずれた知的貢献をしたというよりは、むしろ忍耐力によるものであった。彼は、スルタニエ(Sultanieh)で生まれたペルシアの王子で、天文学と天文表への彼の関心は、彼がサマルカンドに創設した天文観測所の中に示されている。彼の指示で作成された天文表は、東方だけでなく、ヨーロッパでも高く評価された。(29)彼の助手のアル・カーシー(al-Kashi)(30)は、算術と幾何学とについてペルシア語で短い論文を書いた。(31)
これらの名で、イスラム教徒の著述家たちの業績は、事実上、終わる。私たちがこれらの業績をまとめようとするとき、私たちは、アラビア人の学問（科学）への興味と、しかし、独創性の欠如に驚かされる。彼らは、先ず、ヒンドゥーから、そしてギリシアから天文学を受け入れた。彼らの幾何学は、全くすべて代数は主としてギリシアから、そして三角法は、天文学との関連で、大きくヒンドゥーから受け入れた。すでに述べたように(p.177)、彼らは、算術においても幾何学においても、何も重要なものは創り出さなかった。彼らは、代数をある程度体系化し、先行者たちの天文学を改良し、三角法には、いくつか貢献もしたが。これらすべては、相応しい章で議論されるであろう。しかし、全体的に、この時代のアラビア人は、それでも創造者というより、むしろ学問の伝達者であって、彼らの翻訳の中にギリシアの重要な著作の多くが保存されていることから、ヨーロッパ人は、主として彼らに恩恵を受けている。しかし、このかなり大雑把な主張に対して、一つ注目すべき例外が正当に挙げられるだろう。というのは、私たちは、事実上の最初の小数の使用を見るのは、アラビアというよりむしろトルコの学者であるのは、全く確かなことであるように思えるから。この一歩は、ヨーロッパの算術家たちによって、後の時代に、これとは関連なくとられたが、少数は、確かに１５世紀初期にサマルカンドで使用されているように思える。アル・カーシー(al-Kashi)、あるいはイエムシド(Jemshid)(p.289)の著作に、円周と円の半径との長さの比が与えられ、一部、次のように書かれている。
整数
6 28318
それは、小数第16位まで正しい結果である。
正義は、また次のように要求する。800年から始まる４世紀に及ぶアラビア人は、ギリシアの黄金時代の偉大な業績に関してではなく、ヨーロッパや極東の当時の人々の極めて貧しい成果と比較して判断されるべきだと。私たちが、その同じ時代のヨーロッパを考えたとき、数学の分野では、独創的な学者の名はほとんど見いだせないだろう。この時期、アラビア、ペルシア、トルコの学者たちの数は、私たちが知る限り、ヨーロッパの同時代の学者の数を超えているし、彼らの業績の方が意義深いものであった。ヨーロッパの数学が、徐々に発展するようになるのは、1200年から 1400年の間になってようやくのことであり、その時でさえ、アラビアの影響は優れた要因の一つであった。
正義は、さらに要求する。陳述の明晰さのために、バグダッドの学者たちは、およそ６世紀の間、東洋でも西洋でも同時代の人々を凌駕し、独創性においても全く同等であったことを認めることを。