数学史
[14世紀の全般的活動][イタリアの著述家たち][コンスタンチノープル][イギリスの著述家たち][フランスの著述家たち][他の著述家たち]
14世紀の全般的活動
13世紀の学問の復興の輝かしい始まりの後、14世紀は、学問科学と文学との著しい再興を見ることになるだろうと、当然予想される。この予測がなぜ十分に実現されなかったのかを理解するためには、ヨーロッパが直面していた特異な状況を考える必要があるだろう。イタリアに関して言えば、この国は、遂に古代文学の美に完全に目覚め、ダンテ(1265年-1321年)は、自らの師としてヴェルギリウスを語り、「中世(精神)の叙事詩(Epic of Medievalism)」である「神曲(Divina Comedia)」を生み出し、ペトラルカ(1304-1374年)は、古代古典の注目すべき写本集を作り、その結果ギリシアとローマの文学の新しい評価へと行き着くことになる運動を始めた。そして、ボッカッチョ(1313-1375年)は、古代の著作を収集し研究する試みに非常な熱意を示した。この探究において、コンスタンチノープルは、ギリシアの写本のために頼られ、その結果イタリアの学者は、学問(科学)と文学の研究に関心をもった。さらに、フィレンツェ共和国は、1282年と 1292年の間の制度上の改革によって、実際上、商人階級の政府となった。--14世紀の学校におけるフィレンツェの算術が非常に優れていたことと多いに関係があったに違いない事実である。富の全般的な蓄積もまた、それに続いて起こったに違いなく、それは当然、芸術と学問(科学)とを育む傾向があっただろう。これらがすべて約束されていて、その結果が、恐らくルネサンスとして広く知られている時代を早めることになったのだろう。もし、それを阻止する要因がなかったなら。
これらの要因の一つは、百年戦争(1338-1453年、1328-1492年とも言われる)であった。この戦争は、アルプス以北のヨーロッパで最も発達した二つの国の経済的政治的システムを覆した。クレシー(Cresy)の戦い(1346年)は、封建主義以外にも、かなりのものを打ち砕いた。
二つ目の阻む要因は、黒死病(Black Death)の恐るべき猛威であった。それによってヨーロッパの人口の 1/3から 1/2が失われたと考えられている。
14世紀の大学に関していうと、それらは数学にはほとんど寄与しなかった。イタリアの大学は、パリやイングランド、ドイツの同時代の人々に遅れをとっていて、1387年の法規(規則)には、そのテーマ(数学)に関して一言の言及もない。(1)イングランドでは、オックスフォードのマートン・カレッジ(Merton College)が数学の中心であって(2)、この学問をしているふりをしていた。一方、パリは、計算法(algorism)、天文学、幾何学の、そうした学問(数学)の講義があった。新たに設立されたエアフルト大学(University of Erfurt)(1392年)では、そこはドイツ型(の大学)としてとられるだろうが、数学の基本的知識が提供されたが、明らかに求められてはいなかった。(3)
目次へ
イタリアの著述家たち
14世紀のイタリアの著述家の誰も簡単に一瞥するだけで分かるように、数学の何らかの真の天才を示してはいない。チェッコ・ダスコリ(Cecco d'Ascoli)(1257-1327年)は、フランチェスコ・ディ・シモーネ、また、フランチェスコ・デッリ・スタビリとしても知られ、ロマーニャのアスコリ出身であるが、ボローニャとローマの哲学の教授であり、サクロボスコ(Sacrobosco)の「球面幾何学(Sphaera)」について注釈を書いている。(4)また今再び古代の占星術の信仰に高い評価をもたらすのに多くのことをした。占星術は、恐らく、この世紀最大の人気を博していただろう。
アンダロ・ディ・ネグロ(Andalo di Negro)(1260年頃-1340年頃)は、ジェノバの生まれで、数学者、天文学者としてかなりの名声を得、アストロラーベに関するいくつかの著作、惑星についての書物、そして「球面幾何学論(Tractatus de sphaera)」を書いている。また、実用算術も彼のものとされている。(5)
バルラアム(Barlaam)(1290年頃-1348年頃)は、イタリアのカラブリアのセミナラ(Seminara)の生まれで、ゲラチ(Geraci)の司教。コンスタンチノープルで研究し、計算、天文学(6)、数の学問(7)、代数(8)、そしてユークリッドの第2書について著述した。
パオロ・ダゴマリ(Paolo Dagomari)(9)は、トスカナのプラトの生まれで、フィレンツェでは算術家、また天文学者として卓越していた。彼の「算術、天文学、自然と(?)の秘密に関する論(Trattato d'Abbaco, d'Astronomia, e di segreti naturali e medioinali)」は、少し商業算術を含み、彼に学問的というより広い意味での名声を得させている。(10)彼が代数について著述したことは、後の少なくとも一人の著述家によって主張されている。(11)その人物は、この時代に生きていたと言われているパオロ・ピサーノ(Paolo Pisano)であったかも知れない。
数学に関して、一層価値ある著述家は、多くの歴史的覚え書きがある代数の著者(12)、フィレンツェのラファエレ・カナッチ(Rafaele Canacci)(1380年頃)であるように思える。
また、パルマのビアッジョ(Biagio of Parma)(1416年没)(13)もいた。彼は、算術と代数について著述したが、いずれも出版されていない。彼は、パリ、パヴィア(Pavia)、ボローニャ、パドヴァ、ベネチア、そしてパルマで占星術と哲学とを教え、オレスメ(Oresme)の「De latitudinibus formarum」(14)の注釈を書き、静力学(statics)と透視画法(遠近法)について著述した。有名な教育者、ヴィトリーノ・ダ・フェルトレ(1378-1446年、しかし、この年代は疑わしい)は、貧困の中に生まれ、ビアジョの家で、彼から幾何学を学ぶために食器洗いの少年として働いた。そして、やがて、当時の最も優れた数学の教師の一人となった。(15)
その世紀の終わり頃、フィレンツェのアントニオ・ビリオッティ(Antonio Biliotti)(1383年頃)(16)が、ボローニャで数学を教えていたが、彼はそのテーマ(数学)に関して何の著作も残していない。この世紀のイタリアの数学の著作は、それほどのものではなかったが。
目次へ
コンスタンチノープル
この時期、コンスタンチノープルは、黒死病の発生する以前、イタリアで見られたのとよく似た知的復興を経験していた。そうした学者たちの中で卓越しているのは、ギリシアの修道士で、一度ヴェネチアの大使であったマクシムス・プラヌデス(Maximus Planudes)であった。彼は、ディオファントゥスについて著述し、ヒンドゥー・アラビア数字に基づく算術も書いた。(17)彼は勤勉の人ではあったが、天才の人では決してなく、彼の算術は、主として、コンスタンチノープルの数学の思想にバグダードの影響を示していることで価値がある。それは、零と「9つのヒンドゥーから受け継いだ数詞による基数法の体系を示している。そして、現代(近代)の計算法への何らかの関心を向けた最初のギリシアの著作である。プラヌデスは、また、様々なラテンの古典をギリシア語に訳した人として名声に値する。(18)
プラヌデスののマイナーな同時代人の中に、ヨハネス・ペディアシムス(Joannes Pediasimus)(1330年頃)、またガレヌス(Galenus)と呼ばれる人がいた。彼は、アレクサンドリアのヘロンの様式にならって真似しようと試みて書いた幾何学の書を書き、また、立方体の体積を二倍にすることや算術についても著述した。(19)しかし、全般に、彼の著作は文学的哲学的であった。同時代人の間では、彼は「哲学者達の長(Chief of Philosophers)として知られていた。
ヨアネス・ペディアシムスの少し後、コンスタンチノープルに、クレタ生まれの有名な文法学者、マヌエル・モスコプルス(Manuel Moscopulus)(20)がいた。年代は不確かであるが、1300年頃に生きていたように思える。同じ名の人物が二人いるが、この人とその甥である。後で言及するニコラス・ラブダス(Nicholas Rhabdas)による著作の写本から、魔方陣についての論文、地中海の国々で最初にそのテーマについて寄与したものだが、それを書いた人のように思える。(21)
この頃、スミュルナ(Smyrna)のギリシアの「算術家であり幾何学者である」(23)ニコラス・ラブダス(Nicholas Rhabdas)(1341年頃)(22)は、コンスタンチノープルから、算術について、特に、ベーダ(ビード)(Bede)によって何らかの完全さでもって最初に扱われたテーマ、指の数え方(?)(finger reckoning)(24)について二通の手紙を書いている。彼は、また、ヒンドゥーの算術についてのプラヌデス(Planudes)の著作も(25)、恐らく後者の生きている間に校訂(編集)した。彼と共に、かつて、大きなのろしの光であったもの--ギリシアの数学--が明滅し、同時に、言葉そのものの真の評価が存在するのをほとんどやめている。ペトラルカは、1342年に、コンスタンチノープルに住んでいた修道士の助けを借りて、古典ギリシア語を研究し始め、学識ある学者、マヌエル・クリソロラス(Manuel Chrysoloras)は、1397年から 1400年までフィレンツェでその講義をした。しかし、ギリシアの数学的著作がオリジナルの言語で再び知られるようになり始めるのは、16世紀になってからだった。
目次へ
イギリスの著述家たち(26)
イギリスは、この世紀、普通以上の才能をもつ何人かの数学者を生み出した。彼らの一人を除いて、みな疫病の発生の年以前に真の著作を著している。
ウォリンフォードのリチャード(Richard of Wallingford)(1292年頃生まれ、1336年没)は、オックスフォードで自由学芸(liberal arts)について講義し、三角法(27)と算術(28)について著述した。彼は、この時代最もよく知られた数学者の一人であったように思える。(29)ジョン・マンドゥイス(John Manduith)(1320年頃活躍)(30)が彼の足跡を追い、オックスフォードで三角法(31)と天文学とを講義するよう導いたのは、疑いなく彼の影響であった。
14世紀のイングランドの数学者の中で最も優れているのは、「奥深い学者(Doctor Profundus)」として知られる、トーマス・ブラッドワーディン(Thomas Bradwardine)(32)であった。彼は、オックスフォードの神学教授であり、聖パウロ大聖堂の尚書院長(?)(chancellor)であり、リベラリズムの支持者であってカンタベリーの大司教として没した。彼は数学に関して、4つの著作を書いている。彼の「純粋(思弁的)算術(Arithmetica Speculatiua)」(33)では、数の理論とだけ関わる著作であるボエティウスのモデルに従っている。彼の他の著作は、「比例論(Tractatus de proportionibus)」「純粋幾何学(Geometria speclativa)」と「円の求積について(De quadratura circuli)」であった。彼の幾何学には、星の多角形(stellar polygons)(34)、等周図形、比と比例、無理数そして空間の軌跡(loci in space)に関するある著作が含まれている。
この頃、イングランドで、恐らくサマーセットシャー(Somersetshire)のグラストンベリー(Glastonbury)生まれで、リチャード・スィセス(Richard Suiceth)(1345年頃)(35)という名のシトー会修道院の修道士が活躍した。彼は、オックスフォードのマートン・カレッジ(Merton College)で教育を受け、数学に関する余り知られていない著作を書いた。(36)それは、ちょうどイングランドとフランスで注目を引き始めていたテーマ、「図形の大きさ(?)(latitudiuibus formarum)」 を取り扱っている。(37)
この時期、よく知られた著述家、ウォルター・バーレー(Walter Burley)(38)も生きていた。彼の哲学者や詩人たちの生涯に関する著作は(39)、ピュタゴラス、プラトン、プトレマイオスのような優れたギリシアの数学者たちに関する伝記的な記述を含んでいる。
また、14世紀後半には、有名なイングランドの数学者で医者である、サイモン・ブレドン(Simon Bredon)(40)も活躍していた。彼は、天文学(41)、算術(42)、弦の計算(the calculation of chord)(43)、幾何学(44)その他の関連するテーマについて著述し、これらの著作の様々な写本は、まだ存在してる。(45)彼は、三角法に多大な注意を払った最も初期のヨーロッパの学者たちの一人であった。
その時期のマイナーな著述家の中に、マートン・カレッジのウィリアム・リード(William Reade)(46)がいた。彼は数学者としてかなりの名声があり、いくつかの天文表を作成している。また、ウォルター・ブライト(Walter Bryte)(47)は、算術(48)、天文学、外科学について著述したと言われている。
14世紀に、面白いが作者不詳の、高さと距離の測定に関する写本が書かれた。(49)それは、こう始まっている。「これは、地上の物の高さ、深さ、幅を知ることのできる幾何学の論である。(Nowe sues here a Tretis of Geometri wherby you may knowe the heghte, depnes, and the brede of mostwhat erthely thynges)」 それは、コンパスや棒、四分儀(quadrant)を使っての影の測定や測量についての実用的な著作である。そうした多くの著作同様に、それは3部に分かれているが、それは三位一体のキリスト教の思想による可能性が大きい。(50)
かなり関心の高いもう一つの作者不詳の写本、「数える技術(The Crafte of Nombryng)」は、1300年頃書かれた。これは英語で現れた計算(algorism)に関する最初の書の一つである。(51)
目次へ
フランスの著述家たち(52)
戦争と悪疫との災難にもかかわらず、フランスは、国内で生まれた者だけでなく他のどこよりも快適な知的雰囲気をパリに見いだした他の土地出身の学者たちを通して、14世紀ある価値ある著作がなされた。
フランスが養子縁組によって主張できる人々の中に、デンマーク生まれの(54)パリ大学神学校長(rector)で、アラビア記数法(algorism)(55)と教会暦(56)の著作の著者であり、ある(天文)表の編集者(57)であるペトルス・フィロメヌス・デ・ダキア(Petrus Philomenus de Dacia)(53)がいた。また、フランスの養子息子の一人に、ヨハネス・サクソニエンシス(Johannes Saxoniensis)、すなわち、ヨハン・ダンク(Johann Danck)がいた。彼はパリで天文学的著述を続け、天文学について様々な著作を残した。(58)
フランスの生まれた人たちの中で、その時代に相応しい最初の人物は、パリの数学の教授、ヨハネス・デ・リネリイス(Johannes de Lineriis)あるいはジャン・ドゥ・リネール(Jean de Ligneres)(1300年頃-1350年頃)であった。彼はアルフォンソ天文表をその都市の子午線に適用した。(59)ヨアネス・デ・ムリス(Joannes de Muris)あるいはジャン・ドゥ・ムール(Jean de Meurs)(60)は、彼の同時代人で、ソルボンヌで学び、そこで教えた。彼は、算術、天文学、そして音楽について著述した。(1321年) 彼の算術に関する著作のうち(61)--the Canones tabula proportionum, Arithmetica communis ex diui Seuerini Boetij, Tractatus de mensurandi ratione, De numeris eorumque divisione と Quadripartitum numerorum--the Quadripartitum が最も価値がある。それは一部韻文で、ある種の代数を含んでいる。解かれた代数方程式の中に、xx + 12 = 8x その根は2と6; 3x + 18 = xx; そして、すでにアル・フワーリズミーとフィボナッチによって与えられていたもの、(2+7/9)xx = 100 がある。それは、また小数へ近づくアプローチも含んでいる。(62)
この時期、フランスの著述家の中で最も偉大なのは、ノルマンディー生まれのニコレ・オレスメ(Nicole Oresme)(63)であった。一時、彼はパリのコレージュ・ドゥ・ナヴァール(the College de Navarre)の教授で、「偉大なる師(magister magnus)」(1355年)であり、シャルル5世の保護を受け、ルーアンの司教代理(Dean)(1361年)となり、最後には、ノルマンディーのリジュ(Lisieux)の司教(1377年)になった人である。彼は、Tractatus proportionum, Algorismus proportionum, Tractatus de latitudinibus formarum, Tractatus de uniformitate et difformitate intensionum と Traite de la sphere を書いている。彼は、また、アリストテレスの「天と世界(地)について(De coelo et mundo)」を翻訳した。Algorismus proportionum では、分数の指数が初めて用いられたことが知られている。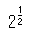 は、
は、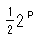 と、
と、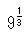 は
は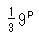 と書かれている。(64)彼は、また数値の8である
と書かれている。(64)彼は、また数値の8である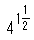 を、
を、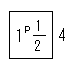 と
と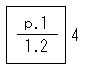 といている。
といている。
Tractatus de uniformitate では、二つの座標によって点の位置を決定することで、座標幾何学への示唆がなされている。(65)オレスメは、また、彼の世代の著しく明晰な思考の経済学者としても優れている。(66)
数学の著述家としてはずっと重要性は劣るが、生涯大きな名声を得た人の中に、パリ大学の神学校長で、カンブレ(Cambray)の司教でもあり枢機卿でもあったペトルス・デ・アッリアコ(Petrus de Alliaco)(67)がいる。彼の天文学に関する著作は(68)、初期の計算法(somputi)にかなりな光を投げかけている。
目次へ
他の著述家たち
この世紀の数学の文献に貢献した他の人々は、全般にフランスやイングランドの人々ほどの才能は持っていなかった。
その世紀の初め、ノルウェーの役人、ハウク・エルレンソン(Hauk Erlendsson)(69)は、アラビア式計算法について書いた。これは、私たちがスカンディナビアで、ヒンドゥー・アラビア算術に関して持っている最初の痕跡である。また、スヴェン師(Master Sven)あるいはスノン(Sunon)というあるスウェーデンの学者もいた。彼は、1340年、球面(sphere)について講義をした。
14世紀の指導的なユダヤの数学者は、レヴィ・ベン・ゲルソン(Levi ben Gerson)(1288-1344年)(70)であった。彼は神学者としてもよく知られていた。彼の「計算機の著作(?)(Work of the Computer)」(71)は、1321年に書かれた。彼は、また、三角法について論文も書いた。(72)それは、「調和の数(?)(De numeris harmonicis)」という題名でラテン語に翻訳されたが、いずれの著作も何ら価値あるものを示してはいない。(73)
イサク・ベン・ヨセフ・イスラエリ(Isaac ben Joseph Israeli)は、明らかにレヴィ・ベン・ゲルソン(Levi ben Gerson)の同時代人であったが、彼の年代については不確かである。彼は、天文学に関する著作を書き(74)、それには幾何学に関する章が含まれ、また、スペインのユダヤとアラビアの学者たちの活動に関する情報の資料としても役立っている。
その時期のマイナーなユダヤの学者の中に、セヴィリャのヨセフ・ベン・ヴァッカー(Joseph ben Wakkar of Seville)(1396年頃)がいた。彼は、トレドのためのある天文表を作成した。ペルジニャンのヤコブ・ポエル(Jacob Poel of Pergignan)(年頃活躍)は、ペルギニャンのために同じことをした。タラスコンのイマヌエル・ボンフィルズ(Imanuel Bonfils of Tarascon)(1377年頃没)は、天文表が高く評価されている人であるが、アストロラーベについて著述している。ヤコブ・カルソノ(Jacob Carsono)(アル・カルシ(al-Carsi))は、セヴィリャとバルセロナで著述し(1375年頃)、その天文表は、ティチョ・ブラヘ(Tycho Brahe)に知られていた。イサク・ザディク(Isaac Zaddik)(アル・シャディブ(al-Shadib))は、アストロラーベについて著述し、天文学者の使用のための様々な表を作成した。また、カロニモス・ベン・カロニモス(Kalonymos ben Kalonymos)は、アルレ(Arles)の生まれで(1286年頃)、カロ師(Master Calo)として知られ、彼の様々な翻訳はニコマコスの一節を含んでいる。
ドイツの著述家の中で、2,3の人が特に言及に値する。これらの最初の人は、ハルバーシュタット(Halberstadt)の司教、ハインリヒ・フォン・ランゲンシュタイン(Heinrich von Langenstein)、ハインリヒ・フォン・ヘッセン(Heinrich von Hessen)すなわちヘンリクス・ヘシアヌス(Henricus Hessianus)(75)であった。彼は、ウィーンで数学を教え、数学者と天文学者としてある名声を得ていた。(76)第二の人は、クンラド・フォン・メゲンベルク(Chunrad von Megenberg)(1309年頃-1374年頃)で、彼はサクロボスコの「球面について(De sphaera)」(77)に基づく著作を書いた(1350年頃)。この頃、もう一人のクンラド(Chunrad)(コンラッド(Conrad))がいて、数学に関心を持っていた。--コンラド・フォン・ユンギンゲン(Conrad von Jungingen)は、写本の一つによれば、「Geometria Culmensis」の著者であったように思える。(78)この著作は、5つの部分からできており、初めの二つは三角形の計量に関するもの、三つ目は四辺形に関するもの、四つ目は多角形、そして五つ目は曲線図形に関するものである。
これらドイツの著述家の最初の二人と同時代の人に、ザクセンのアルベルト(Albert of Saxony)(79)すなわちアルベルトゥス・デ・サクソニア(Albertus de Saxonia)がいた。彼は、プラハ(Prag)とパリで教育を受け、パリ(80)とパヴィア(81)で教えたひとであり、ウィーン大学の最初の学長であり、ハルバーシュタット(Halberstadt)(1366-1390年)の司教となった人である。彼は、いくつかの学問的著作を書いたが、その中に、ボエティウスの方法にならって比を理論的に扱っている(82)「図形の広さについて(De latitudinibus formarum)」(83)「最大と最小(De maximo et minimo)」と「円の求積について(De quadratura circuli)」(84)がある。ほとんどの中世の著述家のように、彼はπの値を、明らかに単なる近似値であるとは思わないで、3+1/7としている。
目次へ
-
原注1
- Suter, "Univ. Mittelalt.," p.75
もとに戻る
-
原注2
- Ibid., p.83
もとに戻る
-
原注3
- W.Hellmann, "Ueber die Anfaenge des math. Unterrichts an den Erfurter ... Schulen, I, 4. Erfurt, 1896.
もとに戻る
-
原注4
- 全般にボローニャの数学者たちについては、Slvestro Gherardi, "Di alcuni materiali per la Storia della Facolta Matematica ... di Bologna, p.17 (Bologna, 1846)を参照。以後、Gherardi, "Facolta Mat. Bologna. として言及する。
もとに戻る
-
原注5
- C.de Simony, Boncompagni's "Bullettino," VII, 313,339.
もとに戻る
-
原注6
- Libri V logisticae astronomicae. また、B.Baldi, "Cronica di Matematici," p.85 (Urbino). と Boncompagni's XIX, 598.を見よ。Barlaam(Barlaamo)の名前は、Bernardoであったかも知れないが、このことは不確かである。彼は、時折彼の生まれた土地から、Calabroとして知られる。
もとに戻る
-
原注7
- Arithmetica demonstratio eorum quae in secundo libro elementorum (Euclidis) sunt. それは、1564年、シュトラスブルクで出版された。
もとに戻る
-
原注8
- Λογιστικη, sive arithmeticae, algebraicae libri VI. これは、1572年、シュトラスブルクで出版された。
もとに戻る
-
原注9
- 1281年頃、Platoに生まれる。1365年か 1374年にフィレンツェに没す。また、Paolo dell'Abaco, Paolo Astrologico, Pagolo Astrologo, Paoli il Geometra, Paolo Geometra, Paolo Arismetra としても知られる。F.Villani (1404年頃活躍)は、Le Vite d'Uomini illustri Fiorentini, 2d ed.,の中で、彼のことを "geometra grandissimo, e peritissimo aritmetico ... diligentissimo osservatore delle Stelle e del movimento de'cieli." 彼の著作の概要は、D.Martine, "Origine e progressi dell'aritmetica," p.59 (Messina, 1865) を見よ。以後は、Martines, "Origine aritmet."として言及する。
もとに戻る
-
原注10
- その著作の描写は、Rara Arithmetica, p.435 を見よ。
もとに戻る
-
原注11
- "m. paolo fiorj che circha al. 1360. duro."に関しての Rara Arithmetica, p.463 を見よ。
もとに戻る
-
原注12
- Rara Arithmetica, p.459 を見よ。
もとに戻る
-
原注13
- また、Biagio da Parma や Pelacani とも呼ばれる。また、1440年頃の写本が主張しているように、「m. biagio che circha al. 1340. anj morj, 」とあるが、この1340年は間違いで、その二つは同じであるかも知れない。Rara, "Arithmetica" p.463 を見よ。
もとに戻る
-
原注14
- p.199を見よ。パリの彼の時代の学生たちには、「aut diabolus est, aut Blasius Parmensis.」というフレーズがあった。
もとに戻る
-
原注15
- W.H.woodward, "Vittorino da Feltre," Cambridge, 1897.
もとに戻る
-
原注16
- また、Antonio dall'Abaco とも呼ばれる。
もとに戻る
-
原注17
- 彼は自分の著作を「Ψηφοφορια κατ' Ινδουs(Indian Arithmetic)」と呼んでいた。C.I.Gerhardt によるギリシア語版(Eisleben, 1865)と、H.Waeschke によるドイツ語訳 Das Rechenbuch des Maximus Planudes (Halle, 1878)(以後、Waeschke,"Planudes"として言及)がある。また、Heath, "History," II, 546.を見よ。
もとに戻る
-
原注18
- Kroll, "Geschichte," p.70.
もとに戻る
-
原注19
- Boncompagni's "Bullettino,"III,303.
もとに戻る
-
原注20
- あるいは、Emanuel. ギリシア語では、その名は、Μανουηλとしても、Εμανουηλ Μοσχοπουλοsとしても現れる。Heath, "History," II, 549.
もとに戻る
-
原注21
- Guenther, "Vermischte Untersuchungen zur Geschichite der math. Wissenschaften," p.195 (Leipzig, 1876) (以後 Guenther, "Vermischte Untersuch.)として言及する); P.Tannery, "Manuel Moschopoulos et Nicolas Rhabdas," Bulletin des Sciences math. el astr., VIII (2), September 2, 1884.
もとに戻る
-
原注22
- Nicholas Smyrnaeus, Rhabda, Artabasda, Artabasdes. 一つの写本には、名前は Nicolas Artavasdan として出てくる。P.Tannery, "Notice sur les deux lettres arithmetique de Nicolas Rhabdas." in Notice et extraits des manuscripts de la Bibliotheque nationale," Paris, XXXII (1886), 121.
もとに戻る
-
原注23
- 彼は自らを描写するときは--"αριθμητικου και γεωμετρου"
もとに戻る
-
原注24
- Εκφρασιs τυ δακτυλικου μετρου. この算術の概要は Bibl. Math., I (2),28 を見よ。それは、数回出版されている。N.Caussinus による "Eloquentia sacra et humanoa," Paris, 1636. と Morellus による "Nic. Smyrnaei Artabasdae, graeci mathematici, "Εκφρασιs Numerorum notationis per gestum digitorum," Paris, 1614. Heath, "History," II, 550.
もとに戻る
-
原注25
- Gerhardt によって 1865年、Eisleben で出版された。
もとに戻る
-
原注26
- Cantor, "Geschichite," II,chap. xlvi
もとに戻る
-
原注27
- Quadripartitum de sinibus demonstratis; De sinibus et arcubus in circulo inveniendo, De chorda et arcu, (and) De chorda et versa. sinibus という言葉は、しばしば sinubus や arcibus として、一般には arcubus として、MSSに現れる。Montucla, "Histoire," I (1),529; Cantor, "Geschichite," II (2),101.
もとに戻る
-
原注28
- De rebus arithmeticis と De computo.
もとに戻る
-
原注29
- 中世の著述家の一人は、彼のことを「in mathesi omnium sui temporis primus」として語っている。
もとに戻る
-
原注30
- Mandwith, Manduit.
もとに戻る
-
原注31
- De chorda et arcu resto et verso, et umbris, は、タンゼントの使用を知っていたことを示している。
もとに戻る
-
原注32
- 1200年頃、Chichester, の Hertfield(Hartfield)に生まれ、1349年8月26日にロンドンの Lambeth Palaceで没す。名は、Bragwardin, Brandnardinus, Bredwardyn, Bradwardyn, de Bradwardina, そして Bredwardina という形で現れる。Pacioli(パチオリ)は(Suma, 1494, fol.68,r.)は彼のことを Tomas beduardin と呼んでいる。
もとに戻る
-
原注33
- 1495年にパリで出版される。
もとに戻る
-
原注34
- "... figuris angulorum egredientibus"
もとに戻る
-
原注35
- 最初の名は恐らく Roger あるいは Raymond であっただろう、そして最後の名は、Suisset, Suicetus, Swincetus, Swineshead, とSuineshevedus である。Northumberland 海岸沖のホーリー島にある、シトー会修道院 Vinshed から派生した言葉。
もとに戻る
-
原注36
- Opus aureum calculationum ... Per ... Iohane de Cipro ... emedat et explicit, s.l.a., but Pavia, 1498. also Pavia, 1498. 初期の著述家に一人によって、"calculator acutissimus" と彼が呼ばれるようになった"calculator"という名で通っているのは、この著作のことかもしれない。
もとに戻る
-
原注37
- Volume II, Chapter V を見よ。
もとに戻る
-
原注38
- 1275年頃オックスフォードに生まれ、1357年頃没す。年代は極めて不確かである。Cantor は、Prantl に従って彼の死を 1337年にしている。ラテン語の綴り、Gualterus Burlaeus と後の英語の Burleighも使われている。
もとに戻る
-
原注39
- De Vita et moribus Philosophorum et Poetarum, 最初に出版されたのは、s.l.a., but Cologne, c.1467. 少なくとも 1501年以前に出版された版が14ある。
もとに戻る
-
原注40
- Winchcomb で生まれ。1386に生きていた。名前は、Bridonus や Biridanus としても現れる。
もとに戻る
-
原注41
- In demonstratione Almagesti.
もとに戻る
-
原注42
- Arithmetica theorica.
もとに戻る
-
原注43
- Calculationes chordarum と Tabulae chordarum.
もとに戻る
-
原注44
- Quadratura circuli per Campanum et Simon Bredon.
もとに戻る
-
原注45
- Suter, "Univ. Mittelalt., 84.
もとに戻る
-
原注46
- Reede, Rede. 彼は 1385年に Chichester の司教として没す。
もとに戻る
-
原注47
- Brithus, Brit, Brytte. 恐らく、ウィクリフ(Wysliffe)の俗人の信徒である Walter Brute と同一人物であろう。
もとに戻る
-
原注48
- Tractatus algorismalis, De rebus mathematicis. 彼のものとされている著作のそれぞれについての出所については、多くの疑いがある。
もとに戻る
-
原注49
- Halliwell, "Rara Math"., 56 そこに完全なテキストが与えられている。MS(写本)は、大英博物館の Bib.Sloan. 213.xiv, fol.120. である。
もとに戻る
-
原注50
- "This tretis es departed in thre. pat es to say. hegh mesure. playne mesure. and depe mesure."
もとに戻る
-
原注51
- この写本のことは、第II巻でさらに完全に述べられる。
もとに戻る
-
原注52
- Cantor, "Geschichte," II, chap.xlvii.
もとに戻る
-
原注53
- 彼のものとされる1300年の東方の計算がある。
もとに戻る
-
原注54
- そこから "de Dacia".
もとに戻る
-
原注55
- Commentum super algorismum prosaicum Johannis de Sacro Bosco. M.Curtz, "Petri Philomeni de Dacia in Algorismum Vulgarem Johannis de Sacrobosco Commentarius," Copenhagen, 1897.
もとに戻る
-
原注56
- Computus ecclesiasticus.
もとに戻る
-
原注57
- 彼の Tabula ad inveniendam propositionem cujusvis numeri は、49*49までのかけ算の表を含んでいる。Bibl.Math., IV (2),32.を見よ。
もとに戻る
-
原注58
- De astrolabio とアルフォンソの表について。Boncompagni's "Bullettino,"XII,352.を見よ。
もとに戻る
-
原注59
- 彼の国籍は確かではないし、彼が Johannes de Liveriis (あるいは Liverius)と同一人物かどうかは明らかではない。彼の分数に関する著作は、1483年、パリで出版された。また、彼はシチリア人であったかも知れない。Rara, "Arthmetica,"p.13; M.Steinschneider, Boncompagni's "Bullettino,"XII,345,352,420 を見よ。
もとに戻る
-
原注60
- 1920年頃、ノルマンディーに生まれる。1360年以降に没す。その名は、Johannes de Murs あるいは de Muria として現れる。L.C.Karpinski, Bibl.Math.,XIII (3),99.
もとに戻る
-
原注61
- 最初の出版は Rara, "Arithmetica"p.117を見よ。また、A.Nagl, "Abhandlungen,"V.135; 彼の著作リストは、p.139を見よ。
もとに戻る
-
原注62
- L.C.Karpinski, "Science"(N.Y.), XLV,663.
もとに戻る
-
原注63
- 1323年頃、恐らく、Caen かその近くに生まれる。1382年7月11日、リジュ(Lisieux)で没す。また、Nicolaus Oresmus, Horem, Horin また Oresmius としても知られる。M.Curtze, "Die Mathematischen Schriften des Nicole Oresme," Berlin, 1870.を見よ。
もとに戻る
-
原注64
- 上で引用した著作の Curtzeによって用いられた、バーゼル大学にある15世紀の写本から。他の MMS は少し異なった形をしている。
もとに戻る
-
原注65
- Cantor, "Geschichte", II, (2),121.
もとに戻る
-
原注66
- Volume II, Chapter V を見よ。Tactatus de latitudinibus の初期の版は、Rara, "Arithmetica" p.117を見よ。また、Zeitschrift (Hl. Abt.),XIII; Bibl.Math., XIII (3),115 と XIV (3), 210 も見よ。
もとに戻る
-
原注67
- Tractatus de origine, natura jure, et multationibus monetarum, edited by Wolowski, Paris, 1864.
もとに戻る
-
原注68
- 1350年、コンピエーニュに生まれる。1420年頃の8月8日に没す。その名は、Pierre d'Ailly, Alyaco,また、Heliaco としても出てくる。Cocordatia astronomie cu theologia. 1490年にアウスブルクで初めて出版される。
もとに戻る
-
原注69
- 1264年頃生まれ、1334年没す。
もとに戻る
-
原注70
- また、Levi ben Gerschom や Gersonides, Leo Ebraeus また Ralbag (RLBGでは Rabbi Levi ben Gerson)とも呼ばれるが、より一般的には、Leo de Balneolis あるいは Master Leon de Bagnolo として知られている。カタロニア(Catalonia)の Balnaolis あるいは Bagnolas で生まれた。J.Carlebach, "Lewi ben Gerson als Mathematiker," Berlin, 1910 を見よ。
もとに戻る
-
原注71
- Maassei Choschelo, edited by G.Lange, Frankfort a. M., 1909.
もとに戻る
-
原注72
- De sinibus, chordis, et arcubus. Bibl.Math., I, (3),372; IV (2),73; XII (2),97.を見よ。
もとに戻る
-
原注73
- Bibl.Math.,XI (2),103.
もとに戻る
-
原注74
- Liber Jesod Olam sive Fundamentum Mundi, 1777年、ベルリンで最初に出版される。
もとに戻る
-
原注75
- 1325年、マールブルク(Marburg)近くのランゲンシュタイン(Langenstein)で生まれる。1397年(時に 1394年とされる)2月11日、ウィーンで没す。
もとに戻る
-
原注76
- Quaestio de cometa. 彼は、また円について書いている。
もとに戻る
-
原注77
- F.Mueller, "Zeittafeln zur Geschichite der Mathematik," p.80. with references (Leipzig, 1892); 以後は、Mueller, "Zeittafeln," として言及する。また、O.Matthaei, "Konrads von Megenberg Deutche Sphaera," Berlin, 1912.
もとに戻る
-
原注78
- Liber Magnifici principis Conradi de Jungegen, Magistri generalis Prusie, geometrie practice usualis manualis," Cantor, "Geschichte," II, chap.xlviii.
もとに戻る
-
原注79
- ザクセン(Saxony)のリッゲンスドルフ(Riggensdorf)に、1325年頃生まれる。1390年、ハルベルシュタット(Halberstadt)で没す。
もとに戻る
-
原注80
- Du Boulay, "Historia Universitatis Parisiensis, p.362. Paris, 1668.
もとに戻る
-
原注81
- F.Jacoli, Boncompagni's "Bullettino," IV,495.
もとに戻る
-
原注82
- Tractatus proportionum, 1478年頃初めて出版された。Rara Arithmetica, p.9.を見よ。
もとに戻る
-
原注83
- 1505年にパドヴァで出版された。
もとに戻る
-
原注84
- F.Jacoli, "Boncompaghni's,"Bullettino," IV,493; H.Suter, "Zeitschrift," (Hl.Abt.), XXIX,81.
もとに戻る
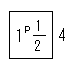 と
と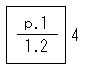 といている。
といている。