数学史

[１３世紀全般の活動][大学の勃興][中世のカリキュラム][レオナルド・フィボナッチ][フィボナッチの他の著作][カンパヌス][他のイタリアの著述家たち][イギリスの学者たち]

１３世紀全般の活動

　１３世紀の数学をどう考えようとも、その世紀が長い知的停滞後の世界の真の覚醒の時代であることは確かである。そのすぐ前の数世紀、ヨーロッパで数学に関する著述家を生み出してはきたが、数学者は一人も産み出してはいない。しかし、今や、その時代の精神があふれ出した。極東では、その影響を感じ、そこから中国では代数の著しい復活発展が見られる。インドもそれを感じ取り、一世代前の、バスカラの優秀さを評価した。そして、知的ヨーロッパのすべてが、これまでになくそれを感じていた。それは偉大なビーコン（水路標識）の光の世紀ではなかったが、西洋のすべての大通りにかけられた灯り、ルネサンスの時代とともに来るべき偉大な啓蒙の約束された世紀であった。₍₁₎

目次へ

大学の勃興

　世界の数学の知識の発展において最も強い影響を及ぼしたのは、もちろんずっと大学であった。私たちが現代の言葉の意味で、これらの組織制度の勃興を跡づけられるのは１３世紀からである。最も初期の中世の大学は、大聖堂、すなわち教会の学校から成長してきたもので、その始まりの年代については、必然的に曖昧になる。しかし、多くの場合、何らかの君主、市民あるいは教会から公に特権を得た年代はわかっており、普通、それらは設立（創設）の年代として受け取られる。時に、二つの年代、国家から特権を得た年代と教会から得た年代とがあることもある。教会は学位のある人たちを教える権利を与えている。こうして、パリ大学は、1200年に国家から許可状を得、その学位は 1283年に教皇によって認められた。それに対応するオックスフォードの年代は、1214年と 1296年であり、ケンブリッジは、1231年と 1318年である。パドヴァ大学は、1222年に創設され、ナポリ大学は、1224年である。₍₂₎１４世紀、１５世紀には、他に多くの大学が創立されるのを見るが、私たちは、１３世紀をこうしたタイプの高等教育の基盤が置かれた時代と見なしている。教えられた数学は、まだ、極めて貧相なものであったが。₍₃₎

目次へ

中世のカリキュラム

　学生は、文法の研究をドナトゥス(Donatus)とプリンキアヌス(Priscian)で始め、アリストテレスから論理学を、キケロから修辞学を学んだ。それから数学的研究に入る。例えば、ボエティウスによる算術、ピュタゴラスによる音楽、ユークリッド（エウクレイデス）による幾何学、プトレマイオスによる天文学と、教会の活動の準備をしていた人々の到達点は、ペテル・ロンバルド(Peter Lombard)の形而上学と神学とであった。この過程は、213ページに示されているように、「マルガリータ・フィロソフィカ(Margarita phylosophica)(1503)」に、グレゴリウス・ライシュ(Gregorius Reisch)によって与えられた知識の塔の中で説明されている。

目次へ

レオナルド・フィボナッチ

　１３世紀最初の偉大な数学者で、事実、中世を通じて最も偉大で最も生産的な数学者は、レオナルド・フィボナッチ、レオナルド・ピサーノ、すなわちピサのレオナルドとしても知られる人物である。₍₄₎
　レオナルドが生まれた時、ピサは、ヴェニス、ジェノバと共に、イタリア最大の商業センターの一つにランクされていた。これらの都市には、商品が蓄えられる大きな倉庫があり、地中海のすべての重要な港では税が支払われていた。そうした施設の長は、かなり著名な人物であった。レオナルドの父₍₅₎が、アフリカの北海岸のブジア(Bugia)₍₆₎で得ていたのはそうした地位であり、この都市でレオナルドはムーア人の校長から初期の教育を受けた。₍₇₎一人の若者として、彼は地中海を旅し、エジプト、シリア、ギリシア、シチリア、そして南フランスを訪れ、₍₈₎学者たちと出会い、様々な土地の商人たちに用いられている様々な算術の大系を知るようになった。しかし、計算のどの大系もすべて、私たちの現代の数詞を用いるものと比較すると、貧しいものと見なし、₍₉₎彼は 1202年に、「算術（算盤）の書(Liber Abaci)」₍₁₀₎という著作を書いた。その中で、彼は、算術と初等代数を満足のいく形で扱っている。その著作は１５の章に分けられ、次の内容の簡単な叙述は、全体の見通しを示すのに役立つだろう。１．ヒンドゥー・アラビア体系の数の読み方、書き方；₍₁₁₎ ２．整数の乗法；₍₁₂₎ ３．整数の加法；４．整数の減法；₍₁₃₎ ５．整数の除法；６．整数と分数の乗法；７．分数のその他の計算；８．物（商品）の値段；９．交換(barter)；１０．協力(partnership)；１１．混合法(Alligation)；１２．問題の解法；１３．仮の立場(?)の規則(Rule of False Position)；₍₁₄₎ １４．平方根と立方根；１５．幾何学と代数、前者（幾何学）は計量の問題である。
　恐らく、彼に自分の名を、時折、レオナルド・ビゴッロ(Leonardo Bigollo)₍₁₅₎と書かせたのは、彼が旅行好きであったからだろう。というのは、トスカナでは、ビゴッロ(bigollo)は、旅行者の意味であったから。その言葉は、また「のろま(blockhead)」の意味もあり、当時の教授たちによってそう呼ばれていたとずっと考えられている。なぜなら、彼は、彼らの学校の出ではなく、彼は学識ある世界に、「のろま」でもできることを示すためだけに、その名を用いて仕返しをしたからである。それは、地方の役人の息子が中世の偉大な数学者になったことを喜ぶことが人間的であるのをちょうど同じように、その後者の説明が正しいものであればよいのにと思うことは、人間的なことであるだろう。フィボナッチの経歴が私たちに警告しているように、そうした著しい経歴の持ち主であった。フルーデ(Froude)が、真に語ったように、「私たちは、占星術に決してたよるべきではない。私たちは、ほとんど何も期待できない。期待するようなことは起こらない。」₍₁₆₎
　レオナルドが数学という学問に新しい光を投げかけていたのと同じ時代に、同じ地域で、キリストの信者の中でも、最も貧しい者、聖フランシスが、人間の魂の中に新しい光を投げかけていた。二人とも、世界の天才の一人であり、天才であるが故になんら人間の説明はいらない。　

目次へ

フィボナッチの他の著作

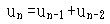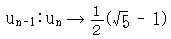　レオナルドは、他に三つの著作、「幾何学の実践(Practica geometriae)₍₁₇₎(1220)」「Liber quadratorum₍₁₈₎(1225)」と「Flos」₍₁₉₎も書いた。その他に、フレデリック２世の哲学者、テオドルス(Theodorus)への手紙が一通現存する。それには、不定分析(indeterminate analysis)や幾何学について述べられている。これらの著作は、ある意味で数の理論を扱っていて、彼の生きた時代を考慮に入れるとレオナルドが、著しい才能のある数学者であったことを示している。彼の名は、０，１，１，２，３，５，８，１３・・・、それはとなるで表される数列（級数）に名付けられている。
　学校に関する限り、レオナルドの著作は、荒野で叫ぶ声のようなものであった。パリ大学の一人の教授も、やがて世界最大の知的中心となるべきものを選び出すのに、Liber Quadratorumの優れた推論から生まれるべきものをなんら作り出すことができなかった、あるいは Flosが精神に伝えようと意味していたことを理解できなかったということは、恐らく真実の範囲にあるだろう。研究の過程は、科学的（学問的）であることとは、ほとんど関わっていなかったので、₍₂₀₎その数学は、そこ、すなわちイタリアの学校には全く立脚点はなかった。

目次へ

カンパヌス

　ロジャー・ベーコンは、この頃生きていたニコラス師(Master Nichokas)という人物、彼に関してはそれ以上のことは私たちは何も知らない、とノヴァリア(Novaria)のカンパヌス師(Master Campanus)についても高い評価をしている。₍₂₁₎後者は、しばらくの間、ウルバヌス４世の礼拝堂付き司祭(chaplain)、ヨハネス・カンパヌス(1260年頃活躍）₍₂₂₎であり、1261年から 1264年まで教皇として支配した。初期に印刷された版のほとんどに用いられたユークリッド（エウクレイデス）の「幾何学原論」の翻訳を準備したのは彼である。しかし、その翻訳は、少なくともそれ以前の３つのアラビア語からの翻訳によっていたように思える。カンパヌスは、また、球面(?)幾何学論(Tractatus de Sphaera)、惑星論(Theoria Planetarum)、暦学(Calendarium)、De Computo Ecclesiastico)という著作、透視画法(perspective)に関する著作、そして、失われたように思えるが、１世紀後のザクセンのアルベルト(Albert of Saxony)(1370年頃)によって言及されている覚え書き(De Quadratura Circuli)を書いている。彼の生涯について、同年代の著述家たちはほとんど語らない。彼は、教会では、比較的マイナーな地位にいた。恐らく、晩年には、パリの司教座参事会員(canon)であっただろう。₍₂₃₎
　ユークリッド（エウクレイデス）の彼の翻訳の付表（補遺）に、星形（五角形）の角の総和の計算方法を示してあった。この時代の占星術師たちによって用いられたその図形が、全般に星形多角形の研究において、様々な著述家によって発展させられた関心事であったことを説明しているというのは、あり得ない話ではない。カンパヌスもまた、三分割の問題(trisection problem)、黄金分割（この名ではまだ知られていないが）の無理数性(the irrationality of the Golden Section)、そして、円とタンゼント（接線）との間の角のことを深く考えた。それ故に、彼は、単なる翻訳した資料の編集者というだけでなく、純粋に幾何学に関心のある人であった。₍₂₄₎

目次へ

他のイタリアの著述家たち

　１３世紀には、イタリアの数学は、ほとんど全く天文学でなりたっていて、このテーマ（天文学）の名を持った著作の中で最も広く知られているのは、バルトロメオ・ダ・パルマの「球面幾何学論(Tractatus Sphaerae)」であった。彼は、1297年、ボローニャで数学を教えていたことが知られている。彼は、また、幾何学と占星術についても書いている。₍₂₅₎
　グリエルモ・デ・ルニス(Guglielmo de Lunis)が、１３世紀に属しているかどうかは定かではないが、₍₂₆₎彼はアラビア語から代数を訳している。₍₂₇₎
　ピエトロ・ダバノ(Pietro d'Abano）₍₂₈₎(1250-1316年頃)は、パドヴァの医学の教授であり、₍₂₉₎Astrolabium planumを書いている。₍₃₀₎彼のアストロラーベへの関心は、疑いなく、それを占星術に応用しようとしたことによるだろう。

目次へ

イギリスの学者たち₍₃₁₎

　フィボナッチは、大学の出ではなかったが、彼は自分の師₍₃₂₎のことをオックスフォードとパリの大学で学んだ人であると語っている。そして、疑いなく、少なくとも大人になってから彼から学んだであろう。この人の名は「魔法使い(the wizard)、マイケル・スコットであり、₍₃₃₎彼は上述の大学で学んだだけでなく、アラビア語を学び、トレドで天文観測を行った。彼は、後に、フレデリック２世に占星術師として任命され、この支配者によって雇われ、アラビア語からの翻訳を通して、新しく発見されたギリシア語のテキストを学者たちに知らしめた。
　マイケル・スコットのようではないが、この時期イングランドで主に研究した人々に何らかの影響が、1224年、オックスフォードにフランシス修道士たちが初めてやってきたことによってもたらされただろう。これらの人々は、₍₃₄₎学問（科学）に博識はなかったが、彼らは南ヨーロッパの知的中心から来たので、アルプスやピレネーの彼方で学者たちがしている事を知らないわけではなかった。大学の中心の一つに彼らがいたということが特に意義深い。

目次へ

原注１

　J.J.Walsh,"The Thirteenth, Greatest of Centuries", New York, 1907.