ブラフマグプタ(Brahmagupta)
７世紀のヒンドゥーの数学者の中で傑出しているのは、ブラフマグプタであった。(1)彼の活動の時期は、天文学的なデータと様々なヒンドゥーの著述家たちとの証言の両方から 628年頃と定められている。(2)彼は、ヒンドゥーの学問の偉大なる天文学の中心、中央インドのグウァリオル(Gwalior)州にある町、ウジジャイン(Ujjain)あるいはウジジャイニー(Ujjayni)で生活し仕事をし、彼の父の統治の間、パトナでアショカ王の太守の地位にあったと言われている。ヴァラーハミヒラもまた、ウジジャインの天文観測所で自らの著作を書いた。
わずか３０才の時に、ブラフマグプタはブラフマシッダーンタ(Brahmasiddhanta)(3)という題名の２１章に及ぶ天文学の著作を書いた。それは、ガニタードハーヤ(Ganitad'haya)(4)とクタカーディヤカ(Kutakhadyaka)(5)という特別の章を含んでいる。前者は、ガナカ(Ganaca)すなわち天文学を研究することが許される（資格のある）計算者の定義で始まる。加法など２０の計算法の他、影による測定法を含む８つの測定法を個別に正確に知っている人がガナカである。(6)
その算術には、整数、分数、数列、交換(barter)、比例、単利（計算）、平面図形の計量、体積や影の計算（彼によって日時計に応用された原始的な平面三角法）の問題が含まれている。計量は時々間違っている。プラフマグプタが、一辺１２の正三角形の面積を 6x12すなわち７２としていたり、10,13,13の二等辺三角形の面積を 5x13すなわち６５としたり、13,14,15の三角形の面積を 7x1/2x(13+15)すなわち９８としていたりするように。彼はまた、どんな四角形の面積も、その四つの辺が a,b,c,dで s=1/2(a+b+c+d)とすると、√(s-a)(s-b)(s-c)(s-d)となるとも述べている。これは、周期的な四角形(syclic quadrilaterals)にだけ当てはまる公式である。彼の四角形のための規則は、次のようなものである。「各辺の合計の半分を４度取り上げ、それぞれ別々に各辺で引き、その答えをすべて掛けあわせたものの平方根が正しい面積である。」(7)彼は、πの「実用的な値」として３を、「きちんとした値」として√１０を用いている。
クタカーディヤカ(Kutakhadyaka)は、代数を天文学の計算に応用している。例えば「与えられた惑星の位置に、どの太陰日(lunar day)あるいは他の測定方法によるどの日、すなわち、週のある特定の日に起こるかを言える人は、粉砕機(pulverizer)に精通している。」(8)
彼の計算についての章では(9)、プラフマグプタは、負の数の一般規則を述べている。彼は、また二次方程式の章もあり、xx+px-q=0のような方程式を解くための規則は、実質的に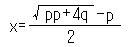
という公式で表されるとも述べている。明らかに、それは一つの解については正しい。
一次の連立方程式の場合、未知数は「色(colors)」として語られ、問題は主に天文学の問題である。実際、プラフマグプタは、私たちの知る限り、最初のインドの著述家であって、代数を天文学に非常に応用した人であった。インドの著作の中に、非常にしばしば見いだされる奇想天外な問題には全般に欠けているが、注釈者は、彼の規則のあるものを例証するのに様々な例を挙げている。そうした二つの問題は、次のようなものである。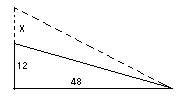
ある丘の上に二人の苦行者が住んでいる。一人は魔術師で空中を進む。山の頂上から跳び上がってある高さまで昇り、隣の町まで斜めに下降する。もう一人は丘の上から歩いて下り、同じ（隣）町まで地上を行く。二人の行程は等しい。私は町から丘までの距離と、魔術師がどれくらいの高さまで昇ったかを知りたい。
注釈者は、ここに示された問題を取り上げ、Ｘは８であると言っている。
１８キューピットの高さの竹が風で折られた。その先端が根から６キューピットの地面に触れている。竹の辺の長さを答えよ。(10)
プラフマグプタが不定方程式の解法に興味があったことは、この時期の代数の状態を暗示している。アーリヤバタは、すでに、ax+-by=cの積分方程式の問題を考えていたが、プラフマグプタは、現実には結果として次のようなものを与えている。
x=+-cq-bt,
y=-+cp+at,
tは、０か何らかの整数で、p/qは、a/bの終わりから２番目の収束(the penultimate convergent)である。(11)彼は、またいわゆる次のような公式の Pell Equationも考えていた。
Duu+I+tt
しかし、その解は、私たちが知る限り、１２世紀のバスカラによって初めて得られたものである。
直角三角形の各辺について、プラフマグプタは二組の数値、
2mn,mm-nn,mm+nn
と
√m,1/2(m/n-n),1/2(m/n+n)
とを与えている。その値は、おそらくギリシアの資料から得られたものだろう。
ブラフマグプタは、国の偏狭な僧侶や無知な民族を喜ばす目的で、科学について虚偽を広めていると非難された。彼は、こうすることで、ソクラテスに降りかかった運命を避けようとしたのであろう。(12)こうしたことすべて、当時、彼が重要人物と認められていたことを示している。
この時代から 1000年まで、北インドでは、学問はほんの少ししか発展しなかったように思える。８世紀に、ラジャプト王朝が高潔なヴァラビスの後を継いだ。そして、2000年の間、インドのこの地域の歴史は空白である。価値ある文学の一つも残っていないし、芸術あるいは産業の著作もない。(13)数学の居場所は、今や北へ移り、２−３世紀の間、ペルシアやムスリムの支配下におかれた他の土地に見いだされる。しかし、南インドでは、マハーヴィーラ(Mahavira)の偉大な著作から見てとれるように、何らかの数学の発展があったに違いない。