算術
ギリシアの計算術であるロジスティックの正確な性質については、ほんの少ししか知られていないが、幸運なことに、数の理論である、ギリシアの算術については、そういうことではない。哲学者たちの主題として、また、哲学者たちによって書かれた著作によって、後のギリシア人たちによって残され、私たちに伝えられてきた。その詳細は、恐らく、初期の時代に伝えられたオリジナルのまま、ほとんど変えられていないだろう。このことについては、私たちの現代の理論の遠い祖先にあたるものでもあり、ロジスティックとともに、第II巻で考察されるだろう。
ギリシアの幾何学
ロジスティックも算術も共に西洋だけでなく、東洋でも発達したが、論理科学としての幾何学は、純粋に西洋文明の産物である。他方、直観的な幾何学は、普遍的なものであり、世界の様々な地域で見られるが、達成段階、達成過程は異なっている。エジプトでは、恐らく、ピタゴラスよりずっと以前に、直角三角形の斜辺の平方の法則(ピタゴラスの定理)を知っていただろう。また、中国とインドでも、それを十分知っていたと信ずる理由がある。しかし、その定理を最初に証明した、また、幾何学的証明の最初の考えを持ったのは、全くギリシア人によるものであることは明らかであろう。事実、命題の論理的な連続と考えている、私たちの幾何学すべては、二次元空間に関するものであれ、三次元空間に関するものであれ、また、円と直線に限定されたものであれ、円錐曲線やより高度な平面曲線を含むものに拡張されたものであれ、その起源は、唯一ギリシア文明の中にあると私たちは考えている。ギリシアの数学は、余りに完全なまで幾何学に専念したので、算術も、ずっと後には代数として知られる学問も、ほとんど全く幾何学的観点から取り扱われた。それ故に、私たちは、ギリシア人の間の数学は、幾何学、算術、ロジスティック、音楽、それに一種の代数を含んでいるとはいえ、中心的要素は幾何学であったと考える。
数学の活動の中心
ミレトスについてはすでに語ったが、更に先に進む前に、ギリシアとギリシアの植民地の他の数学の活動の中心地の位置を確認しておくことが好ましいだろう。次の諸都市と諸国家は、よく言及される。数字は、60ページの地図上の数字を表している。(都市名及び地図は省略)
幾何学的形態に対する初期ギリシアの鑑識
ギリシアは、エジプトやクレタが通過したのと同じ幾何学的形態に対する鑑識の発展段階を通っている。これは、粗雑な平行線から、それほど粗雑ではない平行線へ、そしてより念入りに描かれたもの、更に、最後には、ギリシア芸術の最も高度な発展段階にちょうど先行する時代に発見される、より繊細な形の使用に見られる。これらの幾何学的形態の使用は、特に、ターレスのちょうど前の時代に顕著であった。これは、BC8世紀に頂点に達した、花瓶の装飾の幾何学紋様として知られる。
ギリシアの代数
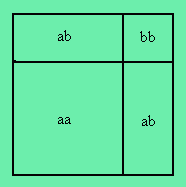
算術や幾何学と区別される学問としての代数は、ギリシアが文明の中心であることをやめた後、しばらく経ってから発明された。しかし、今日、私たちが代数の形で表現しているものと同じものは、ギリシア人にもよく知られていた。それらは、今日、私たちの教科書の中にあるものより、はるかに厳密な証明がなされていた。実際には、そこでは、有理数に限られていた。例えば、事柄を表す代数的な符号もなく、数や積の代わりに、直線と四角形だけで考えたのだけれど、ギリシア人は (a+b)(a+B)=aa+2ab+bb を証明した。同様の仕方で、これらもまた、幾何学的な関係で考えていたけれども、(a+b)(a-b)=aa-bb, a(x+y+z)=ax+ay+az, (a-b)(a-b)=aa-2ab+bb のような他の公式も知っていた。彼らは、二項式 aa+abを表現する四角形を完成することができた。しかし、ここでも、また、四角形を二つにすることで、四角形を大きくしたり小さくしたりすることで作られる幾何学的図形を満たすものと見なされていた。幾何学とは区別される算術の形としてのギリシアの代数は、今、私たちが学んでいる時代よりは幾分後の時代に発達したものである。例えば、ディオファントス(c.275)の生涯と業績について考えるとき、私たちは、後のギリシア人が、この主題の分析的な扱いにおいて、著しい前進を遂げたことを見るであろう。彼らは、かなり優れた象徴主義(記号あるいは符号の採用)を発達させ、「算術」の名の下、私たちがずっと語ってきている幾何学とは全く異なったものとして、代数を考えた。