度数分布の総変動   Total variation of frequency distribution


総変動とは、偏差の平方和のことです。
度数分布の場合、偏差の２乗に度数を掛けて合算して求めます。あるいは、変数の２乗
に度数を掛けて合算し、これより変数の合計（度数込み）と平均の積を引いても、同じ
結果が得られます。
変数が階級に分かれているときは、階級の中央値を階級の代表値とし、計算上の変数と
します。
データの値に単位呼称があるときは、総変動の呼称はデータの呼称の２乗とな
ります。（集団の構成単位そのものの呼称はない（無名）として。）

計算例　次表は、ある果樹園から１季節に出荷された桃の
　　　    重さ（ｇ）の分布です。(階級は、以上−未満)

　　　　　　    階級　　 代表値　　 個数
　　　　     160g-170g    165g　　　93
             170 -180     175      165
             180 -190     185      252
             190 -200     195      318
             200 -210     205      355
             210 -220     215      293
             220 -230     225      176
             230 -240     235      132
             240 -250     245       84
          ------------------------------
            計         -          1868
 
　　　　　桃の重さの総変動は、関連ページにより平均が 203.32976であったので
　　
             {(93*(165-203.32976)2+165*(175-203.32976)2+252*(185-203.32976)2+
             318*(195-203.32976)2+355*(205-203.32976)2+293*(215-203.32976)2+
             176*(225-203.32976)2+132*(235-203.32976)2+84*(245-203.32976)2}
             =777588.81(g2)

          となります。
          なお、変数をそのまま２乗する方法をとれば、

            {(93*1652+165*1752+252*1852+318*1952+355*2052+293*2152+
             176*2252+132*2352+84*2452}-1868*203.329762=777588.81(g2)

          となって、先の計算結果と一致します。

 
　　　−−−−−−−−−−−−−−−−　　　
　　　理論

          Ｋ個のデータ Xi （幅のある階級に区分されているときは、その中央値
          など）とそれぞれに対応する度数 fi が

             X1,X2,....,XK
             f1,f2,....,fK

          であるとき、

           　Σfi(Xi-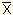)2             (1)
　　　　　　   （Σは iについて 1から Kまで合計する意味。）

        を総変動といいます。この式は

             ΣfiXi2-(ΣfiXi)(ΣfiXi)/F           (2)

        　　　　　（Ｆは各 fiの合計）

        と変形できます。式 (1),(2)は数理的に同じで、どちらを使っても構い
        ません。実務では (2)式がよく用いられます。

        総変動を総単位数 Fで割ったものが分散（基本定義）です。

  ここで参考に（1）式と（2）式が同じものであることを説明します。（1）式の（　）の
部分を２乗して

(1)式=Σf_i(X_i-)²= Σf_i(X_i²-2*X_i +²)= Σf_iX_i²-2*Σ(f_iX_i) +²Σf_i
[[ここで Σ(f_iX_i)=*F, Σf_i=F　ですから]]
=Σf_iX_i²-2*²*F +²*F=Σf_iX_i²-²*F
[[ここで =Σ(f_iX_i)/F に戻して]]
=Σf_iX_i²-(Σ(f_iX_i)/F)*(Σ(f_iX_i)/F)*F=Σf_iX_i²-(Σf_iX_i)*(Σf_iX_i)/F=(2)式
となります。　
−−−−−−−−−−−−−−−−−−−

意味と計算手順のまとめ 意味：総変動は散布度（２次）の一種。 計算手順：偏差の２乗の計として上式 (1)を用いるか、 　　　データの２乗計などを式(2)にあてはめて求める。