度数分布の平均偏差
Mean deviation of frequency distribution


　変数が階級に区分されているときは、計算用の変数は、階級の代表値となります。
　階級の代表値が示されていないときは、階級の中央値などを階級の代表値とします。

　平均偏差は、階級の代表値を変数として、先ず平均を求め、次に変数と平均の
　  差（偏差）の絶対値を作り、それに度数を掛けて合算し、度数の合計で割って
　  求めます。

        計算例　次表は、ある果樹園から１季節に出荷された桃の
　　　    重さ（ｇ）の分布です。(階級は、以上−未満)

　　　　　　    階級　　代表値　　個数
　　　　     160g-170g    165g　　　93
             170 -180     175      165
             180 -190     185      252
             190 -200     195      318
             200 -210     205      355
             210 -220     215      293
             220 -230     225      176
             230 -240     235      132
             240 -250     245       84
          ------------------------------
            計         - 
   
　　　　　桃の重さの平均偏差は、次の様になります。

　　　　　　先ず平均は、関連データより 203.32976であるので
　
　　　　    {93*|165-203.32976|+165*|175-203.32976|+252*|185-203.32976|+
             318*|195-203.32976|+355*|205-203.32976|+293*|215-203.32976|+
            176*|225-203.32976|+132*|235-203.32976|+84*|245-203.32976|}/
                (93+165+252+318+355+293+176+132+84) 
               = 16.6028(g)

          となります。 参考：標準偏差 20.4027(g) 
　　　−−−−−−−−−−−−−−−−　　　
       理論

          度数分布表の階級の代表値 X と度数 f が、

              代表値 X    度数 f 
                  X1         f1
                  X2         f2
                  .          .
                  .          .
                  .          .
                  XK         fK

          のとき、X の平均偏差は

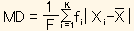                  ={Σf|X-(ΣfX)/F|}/F        (1) 
　　　　　　            （Ｆは各 fiの合計）
  
          となります。 
      -------------------------------



意味と計算手順のまとめ


意味：散布度の１種。

計算手順：１、データから F, ΣfX を求める。

          ２、これらを上式 (1)にあてはめて求める。


      練習問題

        　ある村に、次のような世帯統計があります。
　　　　　世帯人員の平均偏差を求めなさい。

　　　　　　世帯人員規模　　世帯数　　世帯人員
　　　　　　　　　1            52         52
                  2           449        898
                  3          1048       3144
                  4           926       3704
                  5           530       2650
                6-7           270       1728
               8-10            24        205
              11以上　　　　　  1         12

            　    [答 1.0444(人)]   参考：標準偏差 1.3210(人)

　　     　ヒント：世帯人員規模６人以上の階級では、世帯人員を
                   世帯数で割って階級の代表値とします。
　　　
         関連ページ

統計計算例集目次