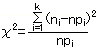χ2検定法の原理

　k個の排反事象があるとき、検定仮説H0として、「それぞれの起こる確率は
p1,p2,p3,.....,pkである。」
とおく。各piはすべて正とする。0が含まれてはならない。合計は当然1とする。
n回の試行の結果、各事象がそれぞれn1,n2,n3,...nk回起きたとし、
かつ、各niが大きいとき、

は自由度k-1のχ2分布に従う。
各niのうち、僅少（5以下など）なものがあるときは、事象を合併して大きくする。
その場合、自由度も下がる。
各排反事象は、区分に意味あるものとする。無意味な細分を行なわない。
各排反事象が度数分布の階級に相当するときは、意味に沿って階級を調整する。階
級は等幅でなくてもよい。

上式のχ2は検定仮説と標本の乖離を示す統計量であり、棄却域を片側右方にとって、
適当な有意水準のもとに、検定仮説の採否を判断する。

問題例1     問題例2

推測統計の基礎

（船津好明）