Ⅰはじめに
スラスト力の計算はパイプラインの設計では不可欠であるが、市販のアプリケーションや表計算ソフトで組んだ計算書を使えば容易に計算可能である。幹支線級の線的な設計では、これらによる標準的な計算で問題ないが、末端配管等の面整備においては、管の分岐や給水栓取り付けがあり、スラスト力の原理を十分理解していないと誤った設計を行う事にもなりかねない。
ここでは、スラスト力を理論だけでなく、動画や図で視覚的に解説し、設計基準で明記されていない部分について考察を行う。
Ⅱ何故スラスト力が生じるか
設計基準「パイプライン」では、スラスト力を次式で求める事としている。
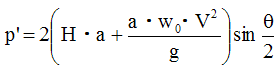
この式は、スラスト力が、水圧の不均衡と、水流の運動エネルギーによる力から成り立っていることを示している。
H・aが水圧の不均衡による力であり、これはパスカルの定理により説明できる。
パスカルの定理
 |
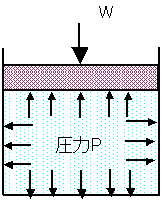パイプラインにおいても同様で、管内に均等に圧力Hが発生する。
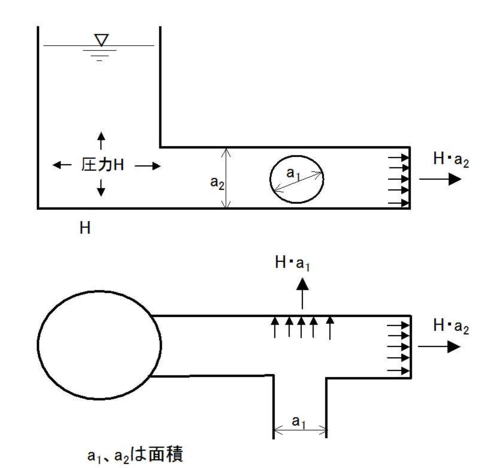
H・a1がT時分岐の時のスラスト力であり、H・a1とH・a2の合力が屈曲部のスラスト力となる。
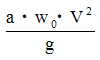が水流の運動エネルギーによる力である。垂直な壁に流量Ｑが流速Ｖで衝突する時、壁に働く力は運動量の方程式より
F=ρQV
となる。
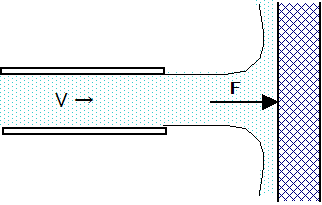
この式が形を変えて水流によるスラスト力を表している。
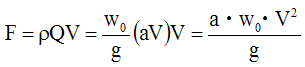
なお、設計基準「パイプライン」では、この水流によるスラスト力は通常の場合、無視して良いとしている。これは、水流によるスラスト力が圧力によるスラスト力に対して無視できるほど小さいとの判断によるものと思われるが、これは”通常の場合”である。
では、通常の場合とは？
明記されていないので判断にとまどうが、この基準で定めている許容設計流速の範囲内であれば”通常の場合”と考えて良いと思われる。
Ⅲスラスト力により何が起こるか
設計基準「パイプライン」には,スラスト力により、管体が振動したり、活動して継手が離れたり、著しい場合には管が破裂することもあると書かれているが、実際の設計では継手の離脱を主に考慮している。そこで、屈曲部及びＴ時分岐部において、継手がどのように離脱するかを見てみる。
まず、一般的な屈曲部で
・スラスト力に対し継手の抵抗力が不足する場合。
こうなる (ブラウザの「戻る」で戻ってください）環境によっては動画が始まるまで時間がかかります
（動画再生にはQuickTimeがインストールされている事が必要です）
曲管両サイドの管の内圧不均衡による力の合力が曲管外側に作用するため、曲管の両方の継手が離脱する。
・継手がTS接合または、離脱防止金具がある場合で、付近に引抜抵抗力の無い継手があった場合。
こうなる
曲管部に抜け止め対策をしても、付近にRR継手のような抜止め機能の無い継手があると、そこが離脱する。この時、この継手までの管と土との摩擦力が曲管に働くスラスト力に抵抗できれば、継手の離脱は起こらない。管の摩擦抵抗力は管の延長によって決まるため、この延長をどれだけ取れば良いかを検討するのが、有効長さの計算や、一体化長さの計算である。
・継手の抜止め抵抗力が十分でなく、付近にキャップ止めがあった場合。
こうなる
曲管がスラストブロックなどで固定されている場合、曲管自体は移動しないが、反力がキャップ止め側に作用するため、こちらが抜け出す。工事の年度割の都合でキャップ止めとする場合、管路末端に給水栓や制水弁がある場合がこれに相当するが、これについても管の摩擦力で抵抗できれば抜けは発生しない。
次に、Ｔ字分岐部について見ると、
・スラスト力に対し分岐側継手の引抜抵抗力が十分でなく、分岐管の摩擦抵抗が小さい時
こうなる
RR継手のＴ字管がスラストブロック等で固定されており、分岐管の延長が短い時などがこれに相当する。
・スラスト力に対し分岐側継手の引抜抵抗力が十分でなく、本管側の受動抵抗が小さい時
こうなる
スラスト要否の検討が行われていれば、このような事例は発生しないことになるが、Ｔ字分岐部の挙動の一つとして取り上げている。
Ⅳスラスト力の対策
スラスト力に対する対策としては、スラストブロック等、構造物によるものと、管路を一体化させて摩擦力と地盤の受動土圧で抵抗する方法がある。後者については、塩ビTS継手のように接着により異形管と管路を一体化させる場合とダクタイル継手や塩ビRR継手のように離脱防止金具を用いる場合がある。実際の設計では、塩ビTS継手の場合、有効長さの計算、ダクタイル継手や塩ビRR継手の場合、一体化長さの計算を行う。
対策工の選定は施工性と経済性を考慮して決定する事になるが、主な判定方針として次のようものがある。
・ＴＳ継手の場合、有効長さが取れない場合のみ、スラストブロックを使用する。
・RR継手の場合、道路下は原則として離脱防止金具、耕地下はスラストブロックとする。（これは、離脱防止金具よりスラストブロックの方が安くなるが、現場打のスラストブロックでは、コンクリート養生期間中、埋戻しが出来ないため道路の通行規制が必要になるからであり、この問題が無い場合は該当しない）
ここで、有効長、一体化長さの扱いや、スラストブロックとの使い分けについては、配管の状況も踏まえて決定する必要があるため、以下に具体的な事例について、スラスト対策の例を示す。
例１
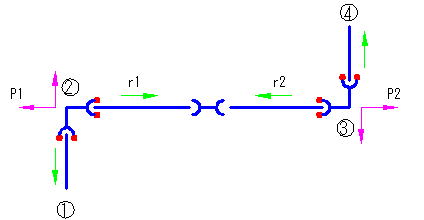
スラスト力 P1, P2 に r1, r2 が抵抗できない場合（一体化長さが取れない場合）、中間のソケット部で抜けが発生する。ここで、r1, r2は管の周面摩擦力と②①、③④部の受動土圧の合計である。
この場合、中間ソケットに離脱防止金具（又はTSソケット）を付けて管路を一体化する。
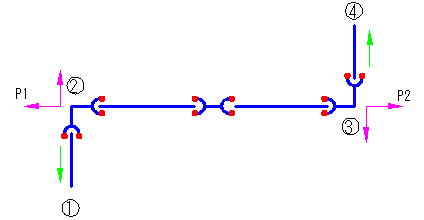
例２
②、③の曲がり角度が異なり、②および③に必要な一体化長さが②-③間に取れなかった場合、どうなるか？
どうもならない（②も③も移動しない）
なぜなら、
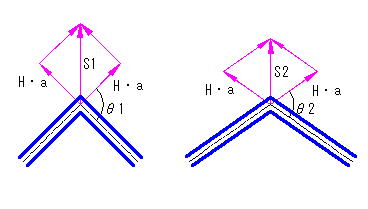
スラスト力Sは曲がり角θにより変化するが、管の軸方向力は常にH・a（内圧×断面積）であり、管径が変わらなければ角度が変わっても変化しない。つまり、上図のP1とP2は等しくなるため、②－③方向の移動は起こらない。ただし①－②、③－④方向については一体化長さが取れている事が前提である。
実際には、、水流の運動エネルギーによる力が加わるため、正確にはP1=P2ではないが、通常の場合、管の周面摩擦等の抵抗力で相殺されると考えられる。
例3
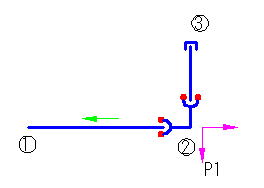
②が離脱防止金具で固定されており、P1に対し②③方向の抵抗力がない場合、②の継ぎ手の抜けは起こらないが、②の移動（滑動）が起こる。これに対する対策としては、②③方向に一体化長さを確保するか、②にスラストブロックを設ける方法がある（下図）。スラストブロックによる場合、②③方向の抵抗力が無いと③側の抜けが発生するので、③側には離脱防止金具が必要である。
例4
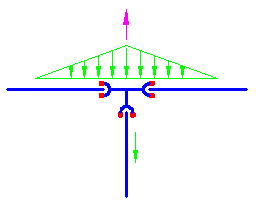
Ｔ字管の３方向に離脱防止金具を設けて一体化すると、分岐管の摩擦抵抗力と、本管側の受動土圧により分岐部は安定する。
分岐管をドレッサージョイント等で既設管に接続する場合、ジョイントに離脱防止機能が無いと、分岐側の摩擦抵抗力が確保出来ない。
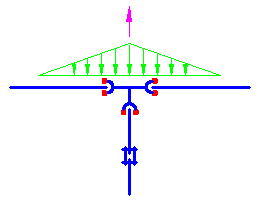
この場合、一体化長さ（又は有効長）の取れる位置にジョイントを設けるか、Ｔ字管にスラストブロックを設ける事が必要である。
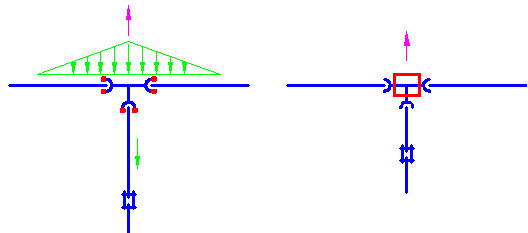
Ⅴ Ｔ時分岐の計算法
有効長さの計算や、一体化長さの計算方法について、設計基準「パイプライン」では屈曲部について解説しているが、Ｔ字分岐部については何も書かれていない。ここでは、Ｔ字分岐部の計算方向について考察してみる。
まず、有効長さの計算について考える。
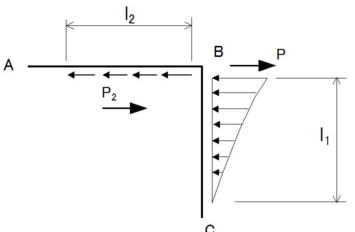
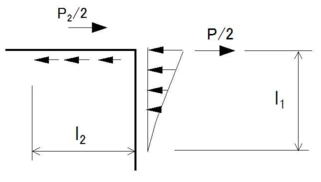
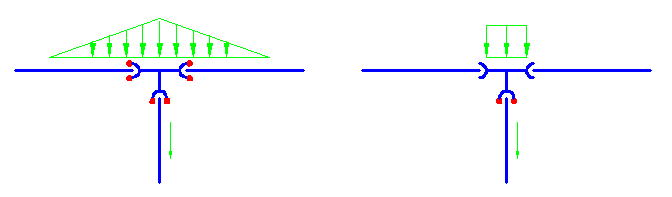
屈曲部の有効長さは上図の l1 , l2 のいずれか大きい方で決まる。
l1は管の曲げ剛度から決まる長さで、外力に関係なく、地盤の特性（地盤反力）と管の材質及び管径が同じであれば一定の値となる。
l2は管の周面摩擦で外力P2に抵抗するための長さであり、P2はBC側の管の曲げ剛性から決まる力でスラスト力のAB方向分力 Pより小さな値となる。つまり、l2 の計算にあたっては、スラスト力に対するl1 間の抵抗力を考慮している。（一体化長さの計算では受動土圧として考慮している）
Ｔ字分岐の場合にも、同様に考えると、力の釣り合いは下図のとおりとなる。
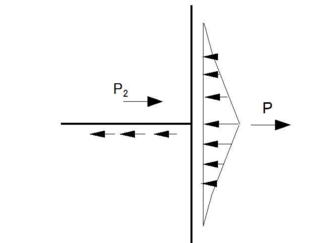
これを拡大すると
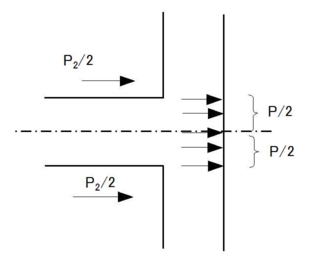
つまり、二つの90°曲がりにスラスト力が配分されると考えることが出来る。
ここで、P2は単純にＰから決まるものではなく、パイプラインP329の式(9.8.34)から計算されるため、α及びβが係わってくる。αは周面摩擦力を含むため分岐側の要素と考えられ、βは曲げ剛度であるため、曲げ反力を生じる本管側の要素と考えられる。二つの90°曲がりに分割する場合、分岐側は半円であるから、αの計算のあたって、管の断面積Asを半円について考え、スラスト力をP/2として計算すると、分岐側に作用する軸力は分割前のP2の半分、つまり P2/2となる。
よって、スラスト力の1/2で90°曲がりの時のl1 ,l2 を求めればよい
l2は次式で求められる。
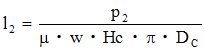
今、P2=P2/2 であり、周面摩擦は半円について考えるから
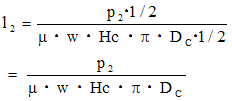
と、もとの式に戻ってしまう。
P2は全スラスト力Pに対応する力であるから、
結局は、全スラスト力Pで90°曲がりとしてl2を求めれば良いことになる。
では、屈曲もＴ字も同じなのか？ そんな事はあり得ない。
実はこれまでの計算で黙認してきた事がある。
それは、l1とP2の計算式である。
前者は l1=π/βで求められるが、これは自立式矢板の値入長の計算と同じで、杭が無限長と見なせる長さを求めている。つまり下図のようなモデルである
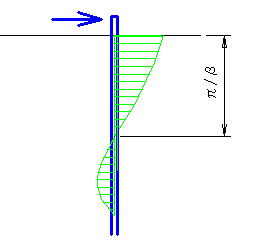
屈曲部の場合はこれでよいが、Ｔ字の場合は自由端が無くなるため、下図のようになる。
理論的な解析は難しいので、FRANE解析によりφ150の塩ビ管について計算してみたところ
上図のLはπ/βの２倍程度になるが、曲げ剛性による抵抗力はＴ字の場合は屈曲の場合の4倍程度になる。つまり、実際にＴ字の分岐部に働く軸力P2は、パイプラインP329の式(9.8.34)で求めたP2より小さくなる。
よって、T字のl2を90°曲がりとして求めると、実際より大きな値になるが、実務的にl2の算出誤差が経済性に与える影響は少ないので、安全側と考えて、この方法によって問題ないと考える。同様の理由によれば、Ｔ字管背面の受動土圧（接続する管は考えない）と分岐管の周面摩擦力を考える方法によっても問題ないと言えるため（塩ビ管小口径の場合、値は90°曲がりとして求めた値と大差ない）、計算の簡略化のためには、これも有効である。
次に、離脱防止金具による一体化長さについて考える。
離脱防止金具による一体化長さの計算では、継ぎ手部をヒンジと考え管の剛性は考慮しない。このため、Ｔ字分岐の一体化長さは、パイプラインP335の式(9.8.49)及び式(9.8.50)において、受動土圧の項を2倍にして求めたL及びL' を分岐側に必要な長さとすればよい。ここで、周面摩擦に関する項は分岐側の管径で、受動土圧に関する項は本管側の管径を使用する。 ただし、この結果を使用するためにはＴ字管の三方に離脱防止金具が必要である。これに対しＴ字管背面のみの受動土圧と分岐管の摩擦抵抗でスラスト力に抵抗できれば、離脱防止金具は分岐管側のみでよくなる。低圧管路で本管に比べ分岐管管径が小さい場合など、このようなケースが多く、塩ビ管用Ｔ字管の製品としても分岐部のみ離脱防止金具付きのものもあるので、これを検討する必要がある。
Ⅵ 管の釣り合い長さ
パイプラインP330 に 「式(9.8.31)のL1,もしくは式(9.8.32)のl2のいずれか大きい有効長に、必要に応じて求めた管の釣り合い長さを加えた長さ以上の連続した埋設長さが必要である」との記述がある。
この“釣り合い長さ”は、p316の式(9.7.3)で求められるものであり、温度変化による管の伸縮量を周面摩擦力によって相殺するに必要な長さである。よって、温度変化が大きい状況が“必要に応じて”の場合に相当することになるが、通常の地中埋設管路でも、この“釣り合い長さ”を考慮して連続埋設長を決定している設計例を時々見かける。しかもこの計算では、温度変化を20℃としている。
一般に地中温度の日変化は地表面が最大で地表面から深くなるにつれてその振幅は急激に減衰する。地表面温度変化30℃程度に対し、地表面から0.25mの位置で3℃程度であるというデータもある（M11．入門２：境界層の日変化の11.5 地中温度の日変化、年変化）。私が学生時代に行った観測でも、地表面下0.60mにおいて気温の日変化がほとんど無い事を確認している。これより、地中に埋設された管路においては、温度変化の影響は考慮する必要はないと考える、まして温度変化20°は、日射の影響をうける構造物の構造計算で考慮する15℃に対し、地中部の温度変化として設定するのは過大と思われる。
そもそも、何故、このような計算が行われているのか疑問に思っていたが、最近、学会から発行されている計算例を見てこの疑問が解かれた。この計算例が温度変化20℃として計算していた。巻頭にかかれている「計算例は理解しやすいように単純なモデルを採用している」の文章は読まれなかったようだ。
Ⅶ 溶着接合部の検討
パイプラインP330に連続埋設長を確保してスラスト対策とする前提条件として、「溶着接合部の強度が軸力以上であること」が挙げられていが、この検討を行っている報告書を見たことがない。そこで、塩ビ管について許容軸力に対応する許容内圧を計算してみたところ、下表のようになった。
| 呼径 φ(mm) |
管外径 d1(mm) |
ソケット長 l(mm) |
許容内圧 σ(Mpa) |
試験水圧に対する比率 σ/2.5 |
| 50 | 60.8 | 63 | 3.5 | 1.38 |
| 65 | 76.6 | 61 | 2.7 | 1.06 |
| 75 | 89.6 | 64 | 2.4 | 0.95 |
| 100 | 114.7 | 84 | 2.4 | 0.98 |
| 125 | 140.85 | 104 | 2.5 | 0.98 |
| 150 | 166 | 132 | 2.7 | 1.06 |
| 200 | 217.9 | 200 | 3.1 | 1.22 |
| 250 | 269.3 | 250 | 3.1 | 1.24 |
| 300 | 320.7 | 300 | 3.1 | 1.25 |
| 350 | 373.1 | 350 | 3.1 | 1.25 |
| 400 | 423.6 | 400 | 3.1 | 1.26 |
| 450 | 474 | 450 | 3.2 | 1.27 |
| 500 | 524.5 | 500 | 3.2 | 1.27 |
上表の試験水圧は、農水管に使われるJIS K 6741 VP の値であるが、これを見ると、所定の仕様に従って施工が行われれば、管の耐力を超える前に継ぎ手が抜け出す事はないことが分かる。よって、通常は検討を行う必要はない。
下の写真は給水栓立ち上がり部の漏水工事で切り出された塩ビ管である。
接着材の円周方向の塗布が均一でなかったか、接着材の劣化の不均等により、スラスト力を受ける面が局部に集中し、管材が引き伸ばされ、管厚が薄くなったところから水が噴き出し穴が空いたものと思われる。これを見ると、継ぎ手の抜け出しと言う面では、接着材の強度は管の材料強度を上まわっていることが伺われる。
Ⅵ 終わりに
コンピュータの進歩によって設計計算は、容易に、スピーディーに行うことが出来るようになったが、我々の技術は経験工学に基づくものである。このため、設計は基準や算式のみで行うのではなく、現象をイメージして体感的に行うべきである。このためには、現場を見る事や実験を行って視覚的に認識する事が重要であるが、現実的には時間の制約や費用面から困難が伴う事が多い。
しかし、一日の仕事を終えて掴む寝酒の入った紙パックでも、工夫次第で、内圧発生装置として、スラスト力で抜ける継ぎ手の様子を再現してくれる。→これ
