側水路式洪水吐安定計算の不思議

2001.10.12 NIKKEI CONSTRUCTION より
| 側水路式洪水吐安定計算の不思議   2001.10.12 NIKKEI CONSTRUCTION より |
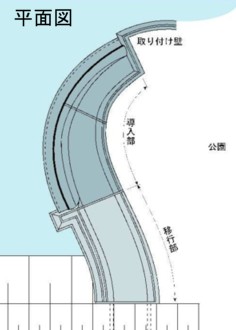
その1. 船に見える? 上の平面図と写真を見て何を感じるであろうか。 私はこんなこんな事に思いを巡らせた。 普通なら設計や施工の手間を考えて堰を直線とするところを、あえて曲線を取り入れたのは何故か?松の木を残したかったのだろうか?水際の曲線美を表現したかったのだろうか? このデザインを提案したのは、コンサルなのか役所の担当者なのか? この側水路の設計は苦労したことだろう、水路には比較的急な勾配がつく上に幅も変化する。このため堰頂の線形を決定するRと堰下流端(水路右岸)のR、及び左岸のRは全て中心位置の異なるRとなる。どのような配筋図を書いたのだろう。 施工も容易で無かっただろう。直線の堰の場合、水糸を張る等すれば堰頂の水平を確保することが出来るのであろうが、このような曲線の場合、堰頂をレベルに保つのは、かなりの手間と技術を要したことと思われる。また、ただでさえ難しいと思われるあのハロルド曲線を平面的な曲線上で施工するのは想像を絶する苦労があったことだろう。 設計者も施工者も苦労した仕事であったと思われるが、その甲斐があって、この洪水吐は覆い被さる松の緑と相まって穏やかな水辺空間の創出に役立っている。 単に堤体を守るだけの地味な水利施設ではなく、人の目を引く景観施設として存在するこの洪水吐の設計に携わった技術者には羨望の念さえ抱いてしまうのは私だけだろうか。 しかし、 会計検査員調査官には、技術者達の努力も美しい景観も胸打つ事はなく、側水路が水に浮かぶコンクリート製の船に見えたそうだ。この奇抜な想像力がコンサルにとって悲劇の始まりとなってしまったのだろう。この事例は、日経コンストラクション(2001.10.12)に「単純ミスの防ぎ方」(第5回 ため池)と題して掲載された会計検査員調査官の報文に挙げられたものである。 調査官は側水路にかかる浮力に関心を持ち、設計でどのように対処しているかを知るために安定計算の提示を求めた。しかし、コンサルは安定計算をしていなかった。現在の水路工では、偏土圧のかかる水路の安定計算について記載しているが、それまでの水路工にはその記載は無かった。現在の水路工が平成13年2月改訂であり、この報文が掲載されたのが同年10月であるから、設計時点では特に基準として示されてはいなかった事と思う。多分、コンサルも役所の担当者も、どっしりとした越流堤と高さの割に幅の広い断面図を見て、これが滑るなどとは思わなかったのだろう。 基準に記載されていなくても安全性の検討は必要である。技術者の「感」では納得出来ない調査官は安定計算を行うことを依頼した。コンサルは時間の捻出に頭を痛め、結果に不安を持ちながら計算をしたことだろう。そして、その結果、滑動の安全率は 常時 0.67 < 1.5 地震時 0.23 < 1.2 であったそうだ。コンサルとしてもこんな数字は出したく無かっただろうから、様々なトライアルの結果なのだろう。 このような数字が出てしまってはもうどうしようもなく、さらに地山側の地下水位と池の水位が連動していることが調査によって示されたため、地山側壁外側下部に暗渠排水、底版にアンダードレーンを設置し、浸透路長確保のために堰前方地中に止水矢板を打ち込む対策工事が行われた。これで、地山側の地下水位が低下して浮力が軽減され、滑動の安全率が確保出来たというのだが、 側水路内は常に空である、 これでは池の水が常に側水路内に浸出しているのではないだろうか? 池に設けられた越流施設を余水吐ということもある。しかし、ため池は先人達が心血注いで築き上げた大事な水の貯留施設であり、余分な水や余った水などは貯えていないとの考えから、ため池では「洪水吐」と言うと聞いたことがあるが、この対策工事では、このことが配慮されていないように思う。そもそもため池改修の必要性に漏水対策があることから考えても、堤体より上流側の水路のFWL以下に水抜きを設ける事は、妥当であるとは思えないのだが、この工法を紹介した調査官はどう考えていたのだろうか。 さらに、もう一つ疑問に思うことがある。コンサルの計算した常時における滑動安全率は0.67である。これは、水路を滑らそうとする力より抵抗力が小さい(しかも7割以下)ことを意味している。 なのに何故、 写真に写っている、ほぼFWLに近い水を湛えた池にあるこの洪水吐は 滑動していないのか? この報文は「ミスを見つけるには、やはり姿、形から感じる直感を働かせる必要があると感じている」と結んでいる。私も、その通りであると思う。調査官は側水路が船に見えた事から浮力の影響に目を付けた事を言っているのだが、断面図を見て、この水路は滑動しないであろうと判断した技術者の直感も、現実に水路が滑動していないことから、まんざら間違いでも無かったように思う。計算結果や設計基準のみで判断して行われた対策工事は、本当に必要だったのか? 本当のミスは、調査官の指摘していない所にあるのではないかと、私は思う。 その2. 壁面摩擦角の不思議 平成13年改訂の水路工では、フルームについても壁面摩擦角の扱いを安定計算時と部材設計時で分けて扱うよう規定している。これは、前述のように、偏土圧の生じるフルームの安定計算の必要性を取り上げた事に対応し、かつ、擁壁の計算との整合性に配慮したものと思われる。ここで、安定計算時の摩擦角の種類を「土と土」としているのは、偏土圧の生じるフルームでは、滑動安全率確保のため、底版張り出し上の土の重量や側壁傾斜上部の土の重量をカウントすることが必要になるため、逆T式擁壁やL型擁壁のように仮想背面を考慮する必要があるとの判断と思われる。さらに基準では、安定計算時の壁面摩擦角算出方法を、側壁の傾斜、底版の張り出しによって区分している。これを示す表には多少分かり辛い点があるが、結局は、背面の土砂重量の効果が見込めない時(基準ではn<0.1 TB<0.10m)、土圧は直接壁面に作用するものとし、 壁面摩擦角を「土とコンクート」として扱うと言うことなのだろう。 以上のような規定があるおかげで、側水路の安定計算が面倒になっている。 通常、側水路の池側の壁(堰前面)は垂直であり、地山側の側壁外側には傾斜、場合によっては底版張り出しがある。このため、地山側の側壁の傾斜及び張り出しの状態によって、壁面摩擦角が変わり、土圧係数算出に当たり、池側と地山の両方を計算しなければならない。 いま、池側壁垂直 地山側側壁傾斜 1:0.1 の時 土の内部摩擦角 φ=30°とすると 池 側 : 壁面摩擦角 δL=20°(2/3φ) 壁背面の傾斜角 θL=90° 地山側 : 壁面摩擦角 δL=30°(φ) 壁背面の傾斜角 θL=90 (仮想背面) それぞれについてクーロンの主動土圧係数を計算すると 池 側 Ka=0.297 地山側 Ka=0.297 不思議なことに、Kaは同じ値になる。 これは決して計算間違いでは無く、答えは同じなのである。 何故か? 理論的に証明するのは難しいので、数値計算で検証してみると
上表は、設計で用いる一般的な内部摩擦角の各々について、壁面摩擦角δ=φとした場合と、δ=2/3φとした場合の土圧係数Kaを比較したものであるが、これを見ると、Kaが同じとなるのはφ=30°の時のみで、他の場合は異なる値になる。つまり、たまたま数字のいたずらで同じ値になっただけのようである。 ちなみに、壁背面の傾斜角を1:0.1に対応する θ=84.29°とした場合
となり、どうやら完全に一致するのはφ=30°θ=90°の時だけのようだが、この場合の方が他のφについてもKaは近い値になる。 では、前の表にもどって、φ=30°θ=90°のときの Kaは同じになるが、安定計算結果はどうなるのか? H=3.0m の壁1.0m当たりにかかる土圧を考えてみる 土の単位重量を γ=18kN/m3 とした時 δ=30°の時の土圧力 P=24.06kN 水平成分 Ph=20.84kN (P・cosδ) δ=20°の時の土圧力 P=24.06kN 水平成分 Ph=22.61kN (P・cosδ) よって、土圧力の差は ⊿P=1.77kN となる ⊿Pに対して、底面摩擦力により滑動の安全率1.5を確保するために必要な鉛直重量Wは f×W/⊿P=Fs より f=0.6 Fs=1.5 として W=Fs・⊿P/f =1.5×1.77/0.6=4.43kN これをコンクリート面積に換算すると A=4.43/24.5=0.181m2 これは、H=3.0mの壁を均等に増やすとすると 0.060m 背面勾配を変えるとすると 0.040勾配を増やすことになる よって、壁厚200が300に、壁面傾斜1:0.1が1:0.15になる可能性がある訳であるから、安定計算に壁面摩擦角が与える影響は大きい。しかし、これは土圧力に対する影響よりも、土圧の水平成分にかかわってくる影響が大きいようである。 その3. 不思議な安定計算例 設計指針「ため池整備」に参考資料として載っている側水路の安定計算に不思議な計算がしてある。 ケースⅢ(緊急放流時)とケースⅣ(地震時満水位)において、滑動安全率が不足したことに対処する計算であるが、両者同様のため、ケースⅢ(緊急放流時)を取り上げると まず ∑V=66.321kN ∑H=25.785kN となったため Fs=(tanφ・∑V+c・B)/∑H =(0.577×66.321+0)/25.785 = 1.484 < 1.5 となった、これは池側壁に主動土圧を考えた場合であるので、池側壁に反力が働く場合を考えて、反力の計算を行っている。 ∑H=25.785-(-1.398)=27.183kN (池側主動土圧を除く) ∑V=66.321-0.509=65.812kN (池側土圧鉛直成分を除く) 反力の計算は、水路工p287の式により P=Fs・∑H - ∑V・f =1.5×27.183 - 65.812×0.577 = 2.801kN この式は、滑動安全率1.5を確保するため、底版摩擦力以外に必要な抵抗力を算出している。 実際に反力として対抗出来る最大の力は受動土圧であるから、このPは受動土圧を上回ってはならない。 受動土圧の計算結果は Ph=61.054kN>P であったので、反力Pは有効として再度安全率を算出している ∑H=27.183-2.801= 24.382kN ∑V=65.812kN Fs=(tanφ・∑V+c・B)/∑H =(0.577×65.812+0)/24.382 = 1.539 > 1.5 不思議である。滑動安全率1.5を確保するためのPを与えた筈なのに、 安全率が1.5より大きくなっている。 この計算の大きな勘違いは ∑H=27.183-2.801= 24.382kN としている点である。P=2.801は安全率1.5を加味した値なのだから、安全率を求めるための∑Hからこれを引いてはいけない。この場合、正しい安全率の算出式は ∑H=27.183kNとして Fs=(tanφ・∑V+P+c・B)/∑H =(0.577×65.812+2.801+0)/27.183 = 1.50 とすべきである。 これについては、水路工p286 に式(7.7.18)として載っている。この「ため池整備」は新水路工より先に発行されているため、その後正誤表や、通達等が出ているのかも知れないが、その点は定かでない。 しかし、ここにはさらなる不思議が潜んでいる たとえば、この場合に底版に張り出しを設け、土重量により底版摩擦抵抗力を増加させた場合を考える。単純に鉛直荷重の増加と考え ∑H=27.183kN (上記から変更なし) ∑V=65.812+3.00=68.812kN (土重量を加算) この時の反力は P=Fs・∑H - ∑V・f =1.5×27.183 - 68.812×0.577 = 1.070kN (受動土圧 Ph=61.054kN 以下) 正しい安全率の算式で計算すると Fs=(tanφ・∑V+P+c・B)/∑H =(0.577×68.812+1.070+0)/27.183 = 1.50 張り出しを設けたにもかかわらず安全率が変わらない 何故か? 考えてみれば当然である。反力の計算は 滑動安全率1.5を確保するため、底版摩擦力以外に必要な抵抗力を算出 しているのである。この値を加えて安全率を計算しているのだから、安全率が1.50以外になるはずは無いのである。 つまり、この考え方では正しい安定計算は出来ない では、どうすれば良いか? そもそも、滑動の安全率とは 滑動させようとする力に対して、抵抗できる力にどれだけ余裕があるかの指標である よって、抵抗出来る力は最大のもので安全率を算術しなければならない。 通常、抵抗できる力の最大は受動土圧となるから ここでの例で計算すると 張り出しを設ける前 Fs=(tanφ・∑V+Ph+c・B)/∑H (Ph:受動土圧) =(0.577×65.812+61.054+0)/27.183 = 3.64 張り出しを設けた後 Fs=(tanφ・∑V+Ph+c・B)/∑H (Ph:受動土圧) =(0.577×68.812+61.054+0)/27.183 = 3.71 となり、張り出しを付けた効果が現れる。 では、常に受動土圧を作用させた計算をすれば良いのか? それについては水路工p285 7.7.3(1)に 「左右岸の土圧作用高さが異なり偏土圧が生じる場合で、その偏土圧が水路底面の摩擦抵抗力以上となる場合は、転倒、滑動、地盤支持の検討が必要である。」 と書いてある。(偏土圧が生じていなくても地盤支持の検討は必要と思われるが、それは置いておいて) この文章に続く (7.7.18)式(上記計算で用いた式と同内容)は、このまえがきの下に有効であるから、安全率の計算に当たってはまずこれを確認しなければならない。 以上の考察より、正しい滑動安全率の算出は次のように行うべきと考える。
|
|||||||||||||||||||||||||||||||||||||||||||