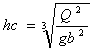
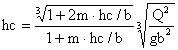
限界水深を語る ●限界水深の算出法 　矩形断面の限界水深は 　　 　又は、単位幅流量に対して 　　 　として計算例などに記載されているが、台形や円形の限界水深の求め方が書かれているものは少ない 　このためか、一般土木の計算書で台形を矩形に近似して限界水深を求めた大胆な設計例を見た事がある。 　矩形断面以外の限界水深の求め方については、水路工p172〜p178に,台形、円形、標準馬てい形の限界水深の求め方が載っている。ここでは、図表を用いることを前提としているが,　限界水深の基礎式は 　 　であるから、台形水路の場合 　 として、上式に代入すると 　限界水深は 　 と表される。　これを解くには逐次計算が必要になるが、表計算ソフトを使えば簡単に解くことができる 円形断面の場合、Aをhの関数で表すと複雑になるため、水路工p177　(6.3.12）式によるのが良いだろう。 ●限界水深の意味 ・フルード数が１となる時の水深 　　Fr＜1の流れが常流　Fr＞1の流れが射流　であり Fr=1となる流れが限界流、この時の水深を限界水深という 　ここで、フルード数とは 　　Fr=V/c で表され、流の流速Vと長波の伝搬速度cの比である。つまり、限界水深は流速が長波の伝搬速度に等しくなる時の水深である。実感として捕らえづらい定義であるが、とにかく限界水深とは 　流れが常流から射流に変わるとき、必ず生じる水深である。 ・一定の比エネルギーのもとに流量を最大ならしめる水深 　水路の一点における比エネルギーは 　　　 と表される。この式においてQとhの関係を求めるとhに対してQmaxが存在する（図.1)、つまりQmaxまでは１つのQに対し2つのhが存在することになるが、この時の多きい方の水深が常流に、小さい方の水深が射流に対応しており、Qmaxとなる水深が限界水深である. 　これより、(∂Q/∂h)E=一定=0として 限界水深の基礎式 　　 　が導かれる。この式は 　常流から射流に変わる流れでは、限界水深によって決定される流量以上は流れない。 　ことを意味している。 ●射流とは 　どこかの大学の先生が、学生たちに「射流とは何か？」と問いかけると「フルード数が・・」とか、「限界水深以下になる時の・・・」と答えることは出来るが、現場に連れて行って「この流れは、常流が射流か？」と聞くと答えられなかったことから、体験して学ぶ水理学の必要性を痛感したと、何かの報文に書いていた。 　確かに自分自身を振り返ると、大学で学んだ水理学より、幼い頃の水遊びのほうが、実際の仕事の上では役に立っているように思う。 　ここで、限界水深に関わってくる「射流」を体感的に把握してみると ・射流は浅くて速い 　感覚的に、流速が遅いと常流、速いと射流といった感じがあるが、矩形断面のフルード数がFr=V/√ghと表されることから、常流、射流の区別は単に流速だけで決まるのではなく、水深と流速の関係で決まることが分かる。 　見た目で判断するなら、水深が浅く、流速の速い流れは射流であると推定できる 　 ・射流は堰上げを起こさない 矩形水路の底面に突起がある場合、常流と射流の水面形状は図.2のように異なった形状を示す。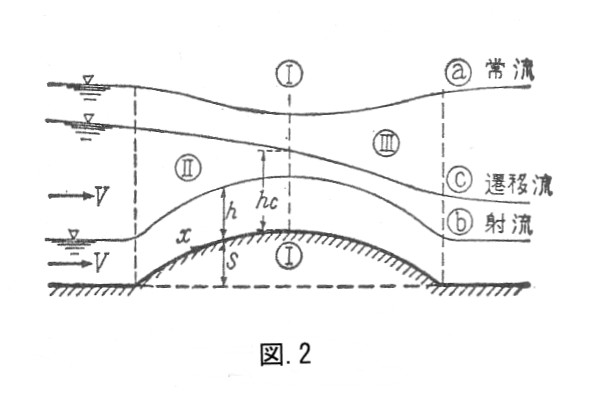 　これは、常流が下流の影響を受けるのに対し、射流は下流からの影響を受けないことが原因となっている。これより、流れの中に大きめの石を置いたとき、上流水位が上昇すれば常流、石に沿った流れになれば射流であると判断できる。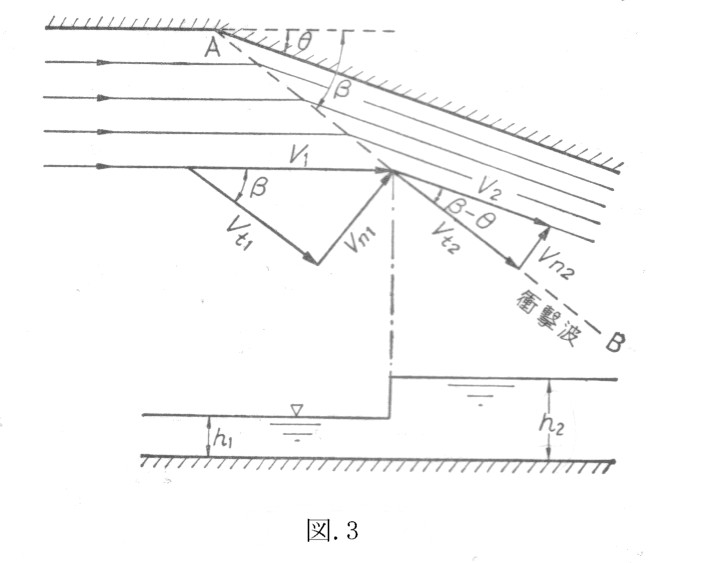 ・射流は衝撃波が発生する 　上記と同様、射流では流れの速度が波の伝わる速度より大きいため、下流側の攪乱の影響は上流に伝わらない。このため、射流が屈曲した水路に流れると図.3のような衝撃波が生じる。これより、水路の屈曲部を見れば、常流か射流かが判断出来る 　 ・射流は跳水する 　射流は下流側の影響を受けないため、下流側が常流となるためには、水位および流速が不連続に変化する跳水現象が発生する。　これは洪水吐の静水池、急流タイプの落差工、水門開時の流出射流に見られる現象である.。 　流れをせき止めて水深を上げたとき、上流水深が渦を伴ってこれより高い下流水深に変化するとき、この流れは射流であると言える。 　　　 ●限界勾配 　等流水深が限界水深に等しくなる勾配を限界勾配という。限界勾配より急な時、流れは射流であり、緩い時、常流となる　 　今、300×300および600×600の断面について、限界水深hc〜流量Q〜限界勾配Icの関係を計算してみると表.1のようになった 表.1 　断　面 hc(m) Q(m3/s) Ic (％) 300×300 0.10 0.030 0.93 0.20 0.084 1.18 0.30 0.154 1.43 600×600 0.20 0.168 0.75 0.40 0.475 0.93 0.60 0.873 1.14 　この表は、たとえば300×300の断面に0.03m3/sの流量が流れるとき、水路勾配が0.93％より急であれば射流 　また、600×600の断面の水深が0.60mの時、勾配が1.14％より急であれば射流であることを表している。 　 この表より、縦断勾配1.5％より急な道路に設置された側溝は、通常の断面規模では、流量の大小にかかわらず常に射流で流れていることが分かる。 ●セキの公式に潜む限界水深 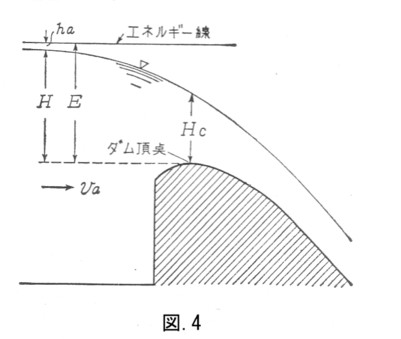　ダム上の流れのように、流れが常流から射流に変わるとき限界水深が生じる。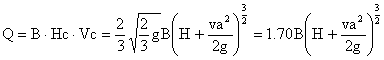　ダム頂点から測った上流水深(越流水深）をH、比エネルギーをE、限界水深をHc、流速をVcとすると、遠心力の影響およびエネルー損失を無視して 　 　また、 　　 　であるから 　　 　実際には遠心力等の影響があるのでこの式を 　　　 　と書き換えたのが、セキの公式の基本型である 　通常のセキの公式は限界水深の生ずる状態つまり完全越流の状態を基本としていることが分かる。 　 ●限界水深は、こう使われる 　・不等流計算の始点水位 　不等流計算は既知の点を始点として、常流の場合は上流へ、射流の場合は下流に向かって計算を進める。この時、流れの途中に支配断面（限界水深の生じる断面）がある場合は、支配断面を計算始点とする必要がある。このため、不等流計算においては、計算方向および始点水位の決定に当たって必ず限界水深を考慮しなければならない。 　・完全越流の判定 　前述のように、セキ上の流れが完全越流となるためには限界水深が存在する事が必要である。完全越流している時、上流側の水位や流量は下流側の影響を受けないが、下流水位が上昇し、限界水深を超える水位になると流量はセキ上下流の水位差に制御されるようになる。この状態のセキは潜りセキといわれ、このときの流量公式は 　　　　 　と表される。これを変形すると 　　　 　となり、セキ上下流の水位差はセキによる損失水頭によって生じている事が分かる。つまり、潜りセキはセキ上下流にベルヌーイの定理の成り立つ連続した流れとなっており、越流量は下流水路の能力に影響される。 　　 　・急勾配水路の断面決定 　　法面に設けられる縦排水溝の断面決定などでは、限界水深で断面決定される場合が多い。これは、縦排水工への流入が常流から射流へと変わる流れであり、このときの流量は限界水深で決定されるからである。一般に水路の断面決定では余裕高を考慮するため、水路高＝限界水深＋余裕高　の条件を満たす限界水深を設定することにより、その水路の流下能力が決定される。 　急流水路の余裕高の取り方には種々の方法があるが、ここでは水深と流速を変数とする水路工P512(8.5.18)式によることとし、300×300および600×600の断面について、流入部の流入可能量と、その流量が法面部（急流部）を流れる時の水深、流速を計算した結果を　表.2に示す 　 表.2　 断面 流入部 急流部 Q(m3/s) hc(m) V(m/s) hc+Fb(m) 法勾配 h(m) V(m/s) hc+Fb(m) 300×300 0.104 0.23 1.50 0.30 1:1.0 0.05 7.54 0.22 1:1.5 0.06 6.68 0.22 600×600 0.586 0.46 2.12 0.60 1:1.0 0.09 11.22 0.43 1:1.5 0.11 10.11 0.45 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ここで、 　　この表から分かるように、流入部の流入可能量は、急流部を同断面とすれば、一般的な法勾配の場合、十分な余裕高をもって流下する。 　 　　一方、水路高＝水深＋余裕高(水路工P512(8.5.18)式による)の条件のもとに、600×600の断面について、勾配別に通水能力を求めてみると表3のようになる 表.3 限界水深より 等流計算より Q(m3/s) hc(m) 勾配 h Qa V Ｆｒ 0.586 0.46 1/50 0.41 0.720 2.927 1.5 斜流 1/75 0.44 0.643 2.436 1.2 斜流 1/100 0.46 0.586 2.141 1.0 限界流 　限界勾配より勾配が急になると、水路の通水能力は限界水深から決定される流量より大きくなる。このため、限界水深で断面決定しておけば、全ての射流状態において安全である。これが、縦排水溝のような急流水路の断面決定の根拠である。しかし、これは水路の流量が水路始点の流入量に支配される場合を前提としている。 　一般の排水路においても急流の場合、限界水深で断面決定している例を見かけるが,水路の側方からの流入の合計を設計流量とする場合では、水路への流入量は限界水深に制限されないため、限界水深で断面決定する事は理論的に不合理である。この場合はそれぞれの勾配に対応する流下能力で断面決定を行うべきである。