| 浮力に弱い示力線方程式 Ⅰ はじめに ブロック積みの安定計算と言えば示力線方程式によるのが一般的であるが、この示力線については ① 岡積 満 の方法 ② 尋木 広義 の方法 ③ 農林水産省の 方法 等があるようである。1) そもそも、示力線は昭和25年に岡積博士によって提案されたもので、岡積の方法ではブロック積擁壁が安全であるためには主働土圧に2倍の安全率を見込んで求められる示力線が擁壁断面の中心点より後方に存在する必要があるとしており 2)、示力線が擁壁断面の中央1/3内にあればよしとする、農林水産省の方法とは考え方が異なっているようである(尋木の方法については資料がないので不明) 我々農業土木の世界で使用する示力線の考え方が、何故、産みの親である岡積博士の方法と異なってきたのかは定かでは無いが、農業土木の設計をする限り、「水路工」に示された方法によっておけば間違いは無いはずである。 ところが、この「水路工」が、とても意地悪で 『ブロック積又はコンクリート擁壁を水路護岸に適用する場合、水路内水位による浮力を考慮してその安全を検討しなければならない』p283 としながらも、示力線の式(p283 式7.7.10)は『浮力の作用しない場合』しか示していない。 では、浮力を考慮するにはどうしたら良いのか? この事を考える前に、まず、実用に供する能力が不十分であるにもかかわらず、ブロック積の安定照査の方法として「水路工」に君臨する、示力線方程式の正体をあばいてみよう。 Ⅱ 示力線の正体は 「水路工」に示される、示力線方程式は次のとおりである 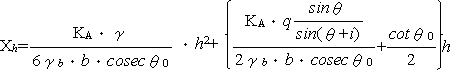 ここで、壁背面の盛土傾斜角 i=0 (地表面水平)の場合を考えると 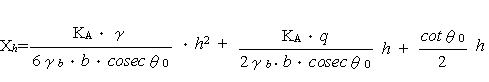 となる。この式は随分スマートになっているが、ダイエットする前の姿にもどしてみると 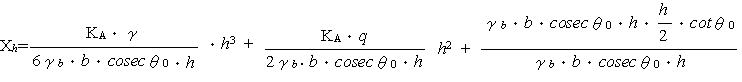 さらにもどすと 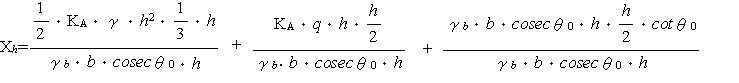 ここまで来ると、見覚えのある算式が現れたのではないだろうか? ここで とおくと M1: 土圧によるモーメント M2: 上載荷重によるモーメント W : ブロック積み重量 である (図.1 参照) この、M1,M2,Wを使って示力線方程式を表してみると 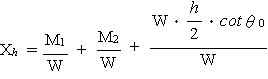 となり、さらにこれに手を加えると 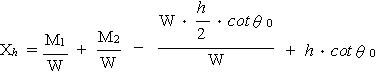 となる。ここで とすると、M3はブロック積み底面中央を原点とする自重によるモーメントであり、式は 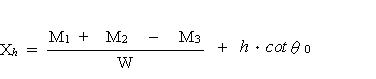 となる。上式中 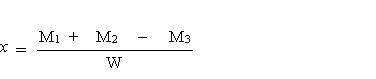 とすると、xはブロック積み底面中央から合力の作用点までの距離であり ブロック積み天端中央からの距離で示される示力線は 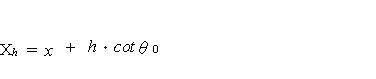 となる。 つまり、示力線は土圧及び上載荷重によるモーメントとブロック自重によるモーメントから高さhの時の底面における合力の位置を求めるのであり、一般の擁壁の安定計算で転倒に対する安定を検討する時、合力の位置を求めるのと同じ事をしているのである。 Ⅲ なぜ示力線なのか では、なぜブロック積の安定計算にのみ示力線を使うのか? これに対する説明としては『ブロック積は一般のコンクリート擁壁と異なり、それぞれのコンクリートブロックが相互のかみ合わせによってその安定を保っているため、ブロック積が安定する為には、ブロックの重量と土圧の合力の示す線すなわち示力線が、全ての位置でミドルサードの前面より後方に無ければならない』などとされている場合が多い。 確かに、ブロック積のブロックは相互に連結されておらず、例え練り積みであっても一体化した構造体とは見すには不十分であるため、理論的にはこのような検討が必要である。しかし、実際に示力線を描いてみると(図.2) 示力線の形状は擁壁背面側に弓形であり限界高さ以浅で示力線がミドルサードの前面にでる事は無い。このため、実務的にはブロック積み底面で通常の擁壁と同様の安定計算を行えば問題無いことになる。実際、示力線で行うブロック積みの安定計算でも底面のみでおこなっているのが殆どである。 こう言ってしまうと、示力線の存在価値が無くなってしまい、示力線法を生み出した岡積博士の努力が酬われない。そこで示力線法のメリットを上げてみると。 ① 公式に数値を代入するだけで、安定性が検討出来る ② ミドルサード前面線と示力線の交点を求める方程式を解くことによって、限界高さが求められる。 ③ 上載荷重や土質に応じて、ブロック積みの高さと勾配を決める選定表等の作成に便利である 等が上げられる。しかし、パソコンで簡単に計算プログラムが作成でき数値計算に手間を要しない現在、残念ながらこれらのメリットに価値は無くなっている。 Ⅳ 示力線が教えてくれるもの 安定計算の手法としては、さほど価値が無いように思われる示力線であるが、ブロック積の力学的なバランスを理解する上では有益である。先に示した示力線の図(図.2)を見ると、限界高さ以浅では下方の一部を除き、示力線は常に壁中央より後方にある。このことは土圧側からのモーメントよりブロック自重のモーメントの方が大きい事を意味しており、ブロック自重を土が押さえている状態であることが分かる。つまり、ブロック積は土留ではなく土に留められている構造体なのである。 さらによく見ると、たとえばブロック積勾配 1:0.5 の時、高さ4.50mのブロック積みでは高さ方向中央部で土側に転倒しようとするモーメントが最も優勢であり、高さ2.50mの時は最深部で最も優勢になる、このように、ブロック積みは高さによって、土側への力のかかり方が変化していることが分かる。このため背面土の一部または全体に抵抗力が不足した場合、ブロック壁体の局部的な変動が全体の力学的なバランスを崩し、ブロック積全体の崩壊を招くことも考えられる。以前テレビでみた、豪雨時の河川で直線部であるにも関わらずブロック積護岸が吸い出されるように崩れ落ちて流されていった映像は、飽和した背面土の強度低下と水位上昇によるブロック前面の水圧増加が原因ではないかと思っているのだが、その真偽は定かでは無い。 Ⅴ 浮力を考慮した検討の方法 先に述べたように「水路工」に示された示力線の方程式は『浮力の作用しない場合』との条件付きであり、浮力を考慮した安定計算には使用出来ない。しかしながら、どうしてもこの式を使いたいらしく、ブロック積と土の単位重量を浮力を受ける部分と受けない部分の加重平均値として計算している例を見かけたが、これは浮力を考慮しているのではなく、『ブロック積なら示力線』という固定観念を考慮しているのだろう。 ここで、正体があばかれたように、示力線方程式は単に合力の作用位置を求めているだけであるため、浮力を考慮した場合の示力線方程式も水深と水中重量の要素を加えれば出来ないことは無い筈である。しかし、前にも述べたとおり、合力の作用位置は一般の擁壁の安定計算と同様にモーメントの釣り合いから求めることが出来るため、表計算ソフト等で計算表を作成すれば、容易に求めることが出来る。(参考例) こうして求めた、浮力を考慮した場合の示力線を示すと 図.3 のようになる。この図に見るように、当然の事ながら、水位が高いほど浮力の影響が大きくなるが、浮力の有無による示力線の形状は同様であり、その開きは下方で顕著である。よって、一般の場合と同様、安定計算は底面部で行えば、それより上の転倒の安全性は全て保証されたことになる。 ここで、「水路工」の場合、土圧係数に水平方向の分力を考慮していない為、市販の擁壁安定計算のアプリケーションソフトで計算した場合、答えが若干異なることもあると思われるので注意が必要である。 Ⅵ おわりに 我々が行う設計計算では、使用する公式や手法によって結果が異なり、構造物規模も異なってくることがある。このため、公共工事として整合性を保つため設計基準等で公式や手法が規定されているが、規定された内容が必ずしも十分でなく実務的に問題を含む場合も多々ある。「水路工」に示されたブロック積の安定計算もこの一つであり、この適用に当たっては、とまどいを覚えた技術者も多いのでは無いかと思う。浮力の検討を明示した現在の「水路工」になってから、既に2年程たっているため、それぞれの形で対応はされているものと思われるが、ここでは、まだこの問題に出会っておらず、これから「水路工」の記述に疑問を持つであろう技術者や、発注者からの質問に答える資料として、何らかの役に立てればと思い、私見をまとめて見た。 これまで、我々の設計は、手段や方法が指定された、いわゆる仕様設計であったが、技術標準の国際化への対応のため、農業土木分野でも、個々の施設ごとに性能を規定し、要求性能を満たしているかどうかを検証する、性能設計の考え方を取り入れる方向で進んでいる。性能設計の世界になれば、示力線方程式は姿を消すであろうし、示力線方程式で説明できない宮勾配や寺勾配などの積み方が採用される場合もあるのかも知れない。そうなれば、設計も面白くなるであろうが、まだ暫くは意地悪な設計基準と付き合うことになりそうである。 参考資料 1)擁壁の計算 Q&A 2)「ブロック積擁壁示力線計算」の解説 |