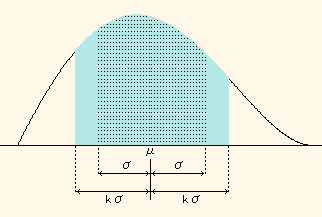チェビシェフ型不等式

（１）平均と標準偏差による分布の分析


 チェビシェフ型不等式を用いると、平均と
 標準偏差を組合わせて、平均の回りの分布
 状況を、構造的に把握することができます。

 チェビシェフの不等式は、任意の正数 k 
 に対して

     Pr(|X-μ|＜kσ)≧1-1/k2

 となります。ここに μは分布の平均、
 σは標準偏差です。

 チェビシェフの不等式は、分布の連続、離散に関わらず、成り立ちます。
 分布に条件がつくと、kσの幅や割合(1-1/k2)が変わり、効率も上がります。
   
 次表の数値は、平均の前後に標準偏差の k倍の幅をとったとき、幅の内側の面積の、全体
 に対する割合を示します。


k=→
1
1.5
2
2.5
3
3.5
条件なし
-
0.56以上
0.75以上
0.84以上
0.88以上
0.91以上
単峰・連続
0.43以上
0.74以上
0.85以上
0.90以上
0.93以上
0.95以上
単峰・連続・対称
0.55以上
0.80以上
0.88以上
0.92以上
0.95以上
0.96以上
正規分布
0.68
0.87
0.95
0.99
0.997
1.000-

上表の「条件なし」はチェビシェフの不等式による評価。

「単峰・連続」はチェビシェフ型不等式の１つであるゼルベルクの不等式による評価。

「単峰・連続・対称」はチェビシェフ型不等式の１つであるガウスの不等式による評価。

これらにより、単峰の連続分布では、平均の周りに標準偏差の２倍半の幅をとれば、
  その中に全分布の９割以上が含まれるといえます。

正規分布のように、分布の型が確定したときは、割合は下限値ではなく、正確な値となります。

統計計算例集目次