変数の取りうる値が2種に限られるとき、その変数は2項分布を するといいます。この場合の値とは、普通の数ばかりでなく、 然・否、 真・偽、 男女の別などの事象や属性も数(値)として 扱います。計算のため、着目する項に1,他の項に0を付与 します。
変数をこのように定義するとき、2項分布の平均は、着目する項の、 全体に対する比(構成比)と同じになります。
 計算例 ある集会に男 45人、女 35人が参加しました。変数を、
参加した各人の男女(男1,女0)の識別のために設定
すると、この変数の取る値はただ2つとなるため、
この変数は2項分布となります。
計算例 ある集会に男 45人、女 35人が参加しました。変数を、
参加した各人の男女(男1,女0)の識別のために設定
すると、この変数の取る値はただ2つとなるため、
この変数は2項分布となります。変数の平均は、1(男)が 45人、0(女)が 35人ですから、
(1*45+0*35)/(45+35) =0.5625 =0.56=56%
となります。 --------------------------------
 理論
理論属性 A または B からなる N 個のデータがあり、 変数 X が A または B を取る2項分布をなすとき、 属性 A に注目してこれに1を対応づけ、属性 B に は0を対応づけるものとします。
X が 1 を取る度数を NA、0 を取る度数 を NBとすると、X の平均は、加重平均と 同じ考え方で、
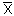 =(1*NA+0*N B)/N=NA/N (a)
(N=NA+NB)
=(1*NA+0*N B)/N=NA/N (a)
(N=NA+NB)となり、Aの構成比に一致します。 −−−−−−−−−−−−−−−−−−−
| 意味と計算手順のまとめ 意味:着目する項 Aの、全項に対する構成比
計算手順:1、データから N, NA, NBを求める。 |
 練習問題
練習問題1800人を対象に、現内閣を支持するかどうか尋ねたところ、 756人が支持、1044人が不支持を表明しました。支持と不支持 の平均を求めなさい。[答 0.42(42%)]
(注)支持に着目して支持者に1,不支持者に0を付与して、 1と0の加重平均をとると、内閣支持率となります。不支 持者に着目すれば、内閣不支持率となります。




















