偏差 Deviation
偏差とは、個々の変数とその平均との差のことです。平均からの偏差とも
いいます。個々の偏差は、集団としての特性値ではなく、ばらつきの要素に過ぎません。
偏差は個々のデータに対するもので、その合計は常に0となります。度数分布に対
しては、個々の偏差に度数を掛けて合計すると0になります。
データの値に単位呼称があるときは、偏差の呼称はデータの呼称と同じです。(集団の
構成単位そのものの呼称はない(無名)として。)
計算例 次の8個のデータ
28,7,11,22,9,16,15,19
の偏差を出してみます。先ずこれらの平均を求めてみると 15.875となるので、
各データと平均の差は、それぞれ、
12.125, -8.875, -4.875, 6.125, -6.875, 0.125, -0.875, 3.125
と8個出ます。これらが偏差です。これらの平均は0となります。
−−−−−−−−−−−−−−−−
 理論
理論
変数 X のとる値を
X1,X2,.....,XN, その平均を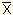 とするとき
とするとき
X1-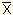 ,X2-
,X2-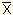 ,.....,XN-
,.....,XN-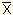
が偏差です。偏差はN個でます。これらの合計は常に0になります。
−−−−−−−−−−−−−−−−−−−
| 意味と計算手順のまとめ
意味:偏差は散布度(1次)の要素。
計算手順:偏差は、個々のデータから平均を引いて出す。 N個出る。
|
 練習問題
練習問題
25 世帯が住むアパートがあり、各世帯の人数は次の通りです。
3, 4, 2, 4, 6, 2, 5, 3, 2, 5,
4, 2, 3, 1, 5, 3, 4, 4, 2, 3,
2, 3, 2, 5, 4
世帯人員の偏差を求めなさい。
[答] 偏差は、平均が 3.32であるので、データの順に
-0.32,0.68,-1.32,0.68,2.68,-1.32,1.68,-0.32,-1.32,1.68,
0.68,-1.32,-0.32,-2.32,1.68,-0.32,0.68,0.68,-1.32,-0.32,
-1.32,-0.32,-1.32,1.68,0.68 となります。





















統計計算例集目次
 理論
理論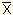 とするとき
とするとき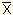 ,X2-
,X2-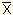 ,.....,XN-
,.....,XN-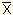
 練習問題
練習問題



















