中心極限定理の例   「中心極限定理」に戻る

例1　矩形分布からの生成

20面のサイコロに0,0,1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10,11,11,12,12,13,13,14,14,15,15,16,16,17,17,
18,18,19,19 と0〜9の数字が2個ずつ記されている。
このサイコロを、1回振る場合、2回振る場合、3回振る場合、4回振る場合、について、各場合の目の平均の確率分布
を調べる。3回以上で正規分布らしく見えることが分かる。
原分布の平均4.5、　分散8.25   赤線は同じ平均、分散の正規分布。

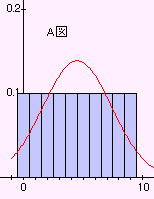
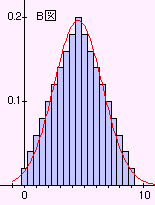
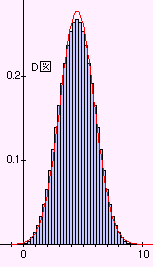A図:1回振り、平均4.5、        B図:2回振り、平均4.5、    C図:3回振り、平均4.5　　 D図:4回振り、平均4.5
    分散8.25（原分布に同じ）      分散4.125                 分散2.75                 分散2.0625                              　　


例2  任意の分布例からの標本平均

　 30 枚のカードがあり、それには次の数字が記されている。

   16,18,20,20,22,22,22,23,23,23,23,23,24,24,24,
   24,24,25,25,25,25,26,26,26,27,27,29,32,33,35

   これより、１枚ずつ独立に１回引く場合、２回引く場合、３回引く場合、４回引く場合、について、各場合の数字の
   平均の確率分布を調べる。
   引く回数が増えるに従って、正規分布に近づくことが分かる。

    原分布の平均 =24.53', 分散 =15.515',  赤線は同じ平均、分散の正規分布。

  
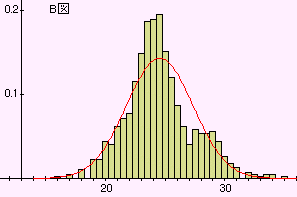  A 図：１回引き、平均 =24.53', 分散 =15.515'(原分布に同じ)     B 図：２回引き、平均 =24.53', 分散 =7.757'

  
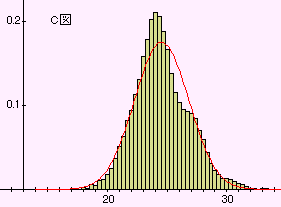
   C 図：３回引き、平均 =24.53', 分散 =5.17185       D 図：４回引き、平均 =24.53', 分散 =3.878'