検定の例1(続) 前頁 次頁
次に対立仮説に対しては、
1回の抽出で赤札が出る確率は2/3、
1回の抽出で白札が出る確率は1/3
となる。このことから、rの確率分布は2項分布となる。
表2及び図1の灰線のようになるが、その基礎となる数値は次のように算出される。
赤札が出る回数(0か1)をr、白札が出る回数(1か0)をwとすれば、赤札がr回、
白札がw回出る確率は、
1Cr(2/3)r(1/3)w,r+w=1,r=0,1
となるから、具体的には
1C0(2/3)0(1/3)1=0.3333
1C1(2/3)1(1/3)0=0.6667
となる。表2の確率分布表は、これに基づいている。
表2 対立仮説に基づく赤札、白札の出る回数の確率分布表
赤札が出る回数 白札が出る回数 出現確率
(r) (w) (p)
0 1 0.3333
1 0 0.6667
計1
( 図1)
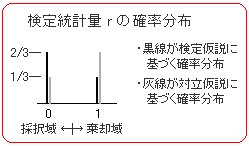 ●仮説の採否の領域
採択域A:赤札が出ない場合。即ち、確率分布におけるr=0の領域。
棄却域R:赤札が出る場合。即ち、確率分布におけるr=1の領域。
(図1参照)
[解説]検定仮説によれば、標本は赤札の方が出にくいから、赤札が出れば標本と
検定仮説の関係が尤もらしくなくなる。そこで、ここでは赤が出たとき検定
仮説を棄却し、赤が出なかったとき、検定仮説を採択することとしたもので
ある。仮設の棄却、採択の領域の決め方は、これに限らないが、ここでは、
例としてこう決めたものである。
●有意水準
この場合、有意水準はα=0.3333(表1より)となる。
[解説]有意水準は、次のように理解する。
「標本の札が赤になることは、検定仮説に基づくそうなる確率0.3333からして、
どちらかといえば起きにくいことである。然るに実際に起きたとすれば、確率
0.3333によるものではなく、仮説とは別の、これを起き易くする何らかの原因
があると考える。」
このように、有意水準は、標本の出現と検定仮説が両立する(しない)と
判断するための確率的水準を示すものである。
●仮説の採否の領域
採択域A:赤札が出ない場合。即ち、確率分布におけるr=0の領域。
棄却域R:赤札が出る場合。即ち、確率分布におけるr=1の領域。
(図1参照)
[解説]検定仮説によれば、標本は赤札の方が出にくいから、赤札が出れば標本と
検定仮説の関係が尤もらしくなくなる。そこで、ここでは赤が出たとき検定
仮説を棄却し、赤が出なかったとき、検定仮説を採択することとしたもので
ある。仮設の棄却、採択の領域の決め方は、これに限らないが、ここでは、
例としてこう決めたものである。
●有意水準
この場合、有意水準はα=0.3333(表1より)となる。
[解説]有意水準は、次のように理解する。
「標本の札が赤になることは、検定仮説に基づくそうなる確率0.3333からして、
どちらかといえば起きにくいことである。然るに実際に起きたとすれば、確率
0.3333によるものではなく、仮説とは別の、これを起き易くする何らかの原因
があると考える。」
このように、有意水準は、標本の出現と検定仮説が両立する(しない)と
判断するための確率的水準を示すものである。
 ●仮説の採否の領域
採択域A:赤札が出ない場合。即ち、確率分布におけるr=0の領域。
棄却域R:赤札が出る場合。即ち、確率分布におけるr=1の領域。
(図1参照)
[解説]検定仮説によれば、標本は赤札の方が出にくいから、赤札が出れば標本と
検定仮説の関係が尤もらしくなくなる。そこで、ここでは赤が出たとき検定
仮説を棄却し、赤が出なかったとき、検定仮説を採択することとしたもので
ある。仮設の棄却、採択の領域の決め方は、これに限らないが、ここでは、
例としてこう決めたものである。
●有意水準
この場合、有意水準はα=0.3333(表1より)となる。
[解説]有意水準は、次のように理解する。
「標本の札が赤になることは、検定仮説に基づくそうなる確率0.3333からして、
どちらかといえば起きにくいことである。然るに実際に起きたとすれば、確率
0.3333によるものではなく、仮説とは別の、これを起き易くする何らかの原因
があると考える。」
このように、有意水準は、標本の出現と検定仮説が両立する(しない)と
判断するための確率的水準を示すものである。
●仮説の採否の領域
採択域A:赤札が出ない場合。即ち、確率分布におけるr=0の領域。
棄却域R:赤札が出る場合。即ち、確率分布におけるr=1の領域。
(図1参照)
[解説]検定仮説によれば、標本は赤札の方が出にくいから、赤札が出れば標本と
検定仮説の関係が尤もらしくなくなる。そこで、ここでは赤が出たとき検定
仮説を棄却し、赤が出なかったとき、検定仮説を採択することとしたもので
ある。仮設の棄却、採択の領域の決め方は、これに限らないが、ここでは、
例としてこう決めたものである。
●有意水準
この場合、有意水準はα=0.3333(表1より)となる。
[解説]有意水準は、次のように理解する。
「標本の札が赤になることは、検定仮説に基づくそうなる確率0.3333からして、
どちらかといえば起きにくいことである。然るに実際に起きたとすれば、確率
0.3333によるものではなく、仮説とは別の、これを起き易くする何らかの原因
があると考える。」
このように、有意水準は、標本の出現と検定仮説が両立する(しない)と
判断するための確率的水準を示すものである。