 円内座標系は、無限に広い直交座標系を有限の円の中に封じ
込めたものです。
円内座標系は、無限に広い直交座標系を有限の円の中に封じ
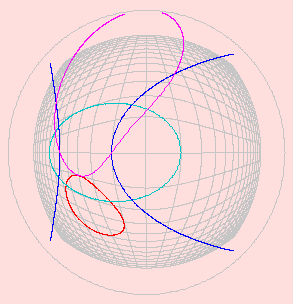
込めたものです。左の円内座標系は、次のように定義されます。 円内座標を (X,Y)、普通の直交座標を (W,Z) として
W=a*X/(√(X2+Y2)+b) Z=c*Y/(√(X2+Y2)+d)
ここに、a, c は a=cで円の半径、b, d は目盛の調整値で、すべて正数とします。 左図では a=4, b=3, c=4, d=3 です。 aと cが等しくないときは、楕円となります。 更に b, dを変えることによって、目盛の伸縮ができます。
図の外側の円は、普通の直交座標系における無限遠線に当たります。 図の外側の円のすぐ内側が空白となっているのは、普通の直交座標系の原点から非常に遠い位置に当たるため、 描画を省略したためです。
円内座標系においては、任意の2つの数の組 (X,Y) と、座標系内の点とは、1対1の対応をします。
赤:(X+3)2+(Y+3)2=4
水色:(X+3)2/16+Y2/4=1
青:(X+3)2-Y2=4
紫:Y=(X+3)2/4-1
閉鎖座標系の目次 座標系とグラフ 先頭ページへ