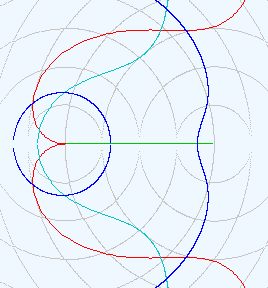
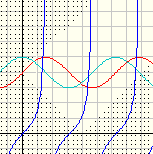
 左:2円座標系、上:直交座標系
左:2円座標系、上:直交座標系2円座標系の X 座標は左円の中心からの距離、Y 座標は右円 の中心からの距離です。
上の直交座標系の影の部分は、この2円座標系には反映されま せん。
この2円座標系と直交座標系の関係は、2円座標を (X,Y)、直交座標を (W,Z)とすると、
W=(X2-Y2)/(4*a) Z2=-(X2-Y2-4*a*X+4*a2)*(X2-Y2+4*a*X+4*a2)/(16*a2)
X≧0, Y≧0, X+Y≧2*a, |X-Y|≦2*a, a≧0 ここに、2*a は2つの円の中心間の距離(緑線)で、 図では a=2 です。目盛の単位 1。
2円座標系のグラフは、必ず上下対称になります。
赤:Y=Sin(X)+4(4を取り去ると、原図が影の中に入り、2円座標系に軌跡がでません。)
水色:Y=Cos(X)+4(上に同じ)
青:Y=Tan(X)
(座標の位置の例は設定例を参照。) 座標系とグラフ 方程式とグラフ 先頭ページへ