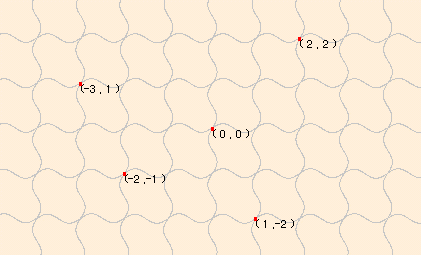
関数座標系は、直交座標系との関係式 によって決まり、種類は無数にあります。 極座標系なども、実は関数座標系の1種 です。 左の関数座標系は、次のように定義されます。 関数座標を (X,Y)、直交座標を (W,Z) とし て、両者の関係を次式で規定したものです。
W=X+a*Sin(b*Y), Z=Y+a*Sin(b*X) ここに、a は座標の揺れ幅の係数で、 0 に近いほど直交座標系に近くなります。 b は揺れの周波の係数で、大きいほど高 周波になります。 左図では a=0.1, b=2 です。
この座標系を、揺らし座標系ともいいます。
関数座標系においては、任意の2つの数の
組 (X,Y) と、座標系内の1点とは、必ずしも1対1の対応をしません。図の例では、a が 0 に近ければ、 1対1の対応をします。
関数座標系と直交座標系の関係は、一般に
W=F(X,Y), Z=G(X,Y)
あるいは
F(X,Y,W)=0, G(X,Y,Z)=0
あるいは
F(X,Y,W,Z)=0, G(X,Y,W,Z)=0
で表わされます。
座標系とグラフ 方程式とグラフ 先頭ページへ