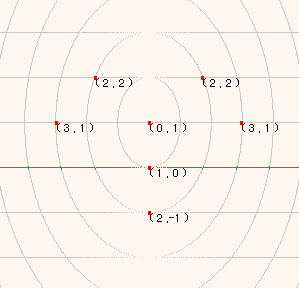
楕円焦準座標系は、直交座標系との関係式 によって何通りもできます。 左の楕円焦準座標系は、次のように定義されます。 楕円焦準座標を (X,Y)、直交座標を (W,Z) とし て
W2=b*{X2-(Y-a)2}, Z=Y 0≦X, -X+1≦Y≦X+1
ここに、a は焦点、b は楕円化の係数で、 左図では a=1, b=1/2 です。(b=1は円、 0<b<1 は縦長楕円、b>1 は横長楕円)
X座標は焦点 (0,1) からの距離、Y 座標は 準線(緑線)からの距離です。方程式 Y=X は 放物線となり、その焦点は(0,1)、準線は Y=0(緑線)です。 楕円焦準座標系においては、X<0 は認めません。
楕円焦準座標系においては、任意の2つの数の
組 (X,Y) と、座標系内の1点とは、必ずしも1対1の対応をしません。 楕円焦準座標系のグラフは、必ず左右対称になります。
座標系とグラフ 方程式とグラフ 先頭ページへ