極座標系は、設定の仕方によって何通りも
できます。

以下の説明の順序は、２次元座標系設定の
一般原理の説明順に合わせてあります。

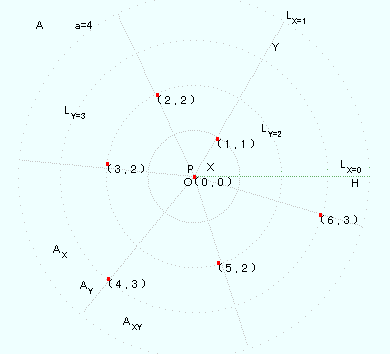
(1) 座標系を設定したい面を、平面 A と
  します。
　平面 A の上に、長さ a (a＞0)の直線分
  ＯH を引き、Ｏ→H の方向（左から右）
  に、0 から a に亘って等目盛を印します。
  Ｏを極といいます。極は P とも書きます。

(2) 2つの変数を X,Y と置き、これらを座
  標変数とします。

(3) X の変域を 0≦X＜2π とし、変域内の
  １つの X に対して長さ a の直線分 LX
  を、その一端を極 P におき、直線分
  ＯH と逆時計方向に　X 角をなすように
  引きます。

(4) X が 0 から 2π の間を連続的に変化するとき、直線分 LX も A の上を連続的に移動しま
  す。

(5) LX の移動の軌跡は、平面 A の上に半径 a の円の内部 AX を形成します。

(6) Y の変域を 0≦Y＜a とし、変域内の１つの Y に対して、中心 Ｏ、半径 Y の円 LYを描き
  ます。

(7) Y が 0 から a の間を連続的に変化するとき、円 LYも A の上を連続的に変化します。
  LY=0 は極 Ｏに一致します。

(8) LY の変化の軌跡は、平面 A の上に半径 a の円の内部 AY を形成します。

(9) こうして得た A の上の２つの領域 AX と AY の共通部分を AXY とします。この場合、
  AY は AX に含まれるため、AXY の領域は AY の領域と同じになります。
  a=∞ のとき、普通にいう極座標系と同じものになります。

(10) この極座標系内の１点 Q は、極を除けばただ１つの LX の 上にあり、かつ、ただ１つの
  LY の上にあり、その座標は (X,Y) とただ１通りに表わされます。
  極の座標は、(X,0) の形で無数にあります。
(11)-
(12)-
(13) 0≦X＜2π, 0＜Y＜a において、２つの数からなる組 (X,Y) を作ると、これを座標とする
  点 Q が、座標系内にただ１つ定まります。

(14) a=∞ におけるこの極座標系と直交座標系の関係は、次の通りです。
  極座標を (X,Y)、直交座標を (W,Z)とすれば、

      W=Y*Cos(X),   0≦X＜2π
      Z=Y*Sin(X),   Y≧0
         (Y＜0 を認めないことに注意)

  となります。

座標系とグラフ   方程式とグラフ   先頭ページへ