 埲壓偺愢柧偺弴彉偼俀師尦嵗昗宯愝掕偺堦斒尨棟偺愢柧弴偵崌傢偣偰偁傝傑偡丅
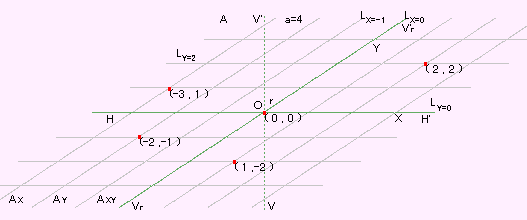
埲壓偺愢柧偺弴彉偼俀師尦嵗昗宯愝掕偺堦斒尨棟偺愢柧弴偵崌傢偣偰偁傝傑偡丅(1) 嵗昗宯傪愝掕偟偨偄柺傪丄暯柺 A 偲偟傑偡丅
嘆 暯柺 A 偺忋偵丄挿偝 2a (a亜0)偺捈慄暘 HH' 傪堷偒丄H仺H'(嵍偐傜塃)偺曽 岦偵丄-a 偐傜 a 偵榡偭偰摍栚惙傪報偟傑偡丅 丂 嘇 捈慄暘 HH' 偺忋偺 a=0 偵憡摉偡傞埵抲傪 俷(蛋)偲偟丄俷偵偍偄偰 HH' 偲 捈岎偟 俷 偵傛偭偰俀摍暘偝傟傞挿偝 2b (b亜0) 偺捈慄暘 VV' 傪堷偒傑偡丅 丂 嘊 俷傪捠傝丄VV' 偺惓偺懁偐傜帪寁曽岦偵 r 妏傪側偡挿偝 2b 偺捈慄暘 VrV'r 傪丄俷偵傛偭偰俀摍暘偝傟傞傛偆偵堷偒丄Vr仺V'r(嵍壓偐傜塃忋)偺曽岦偵丄-b 偐傜 b 偵榠偭偰摍栚惙傪報偟傑偡丅偙偺応崌丄HH' 偺忋偺栚惙偺広偲丄VrV'r偺 忋偺栚惙偺広偲偼堎側偭偰傕峔偄傑偣傫丅 丂 嘋 捈慄暘 VrV'r 偺忋偺 b=0 偵憡摉偡傞埵抲偼 俷 偵廳側傝傑偡丅俷 傪尨揰偲偄偄 傑偡丅
(2) 2偮偺曄悢傪 X,Y 偲抲偒丄偙傟傜傪嵗昗曄悢偲偟傑偡丅
(3) X 偺曄堟傪 -a亙X亙a 偲偟丄曄堟撪偺侾偮偺 X 偵懳偟偰丄挿偝 2b 偺捈慄暘 LX 傪丄捈慄暘 HH' 偺忋偺 X 偵憡摉偡傞栚惙偺埵抲偵丄HH' 偵傛偭偰俀摍暘偝傟丄 偐偮 VrV'r 偵暯峴偲側傞傛偆偵堷偒傑偡丅
(4) X 偑 -a 偐傜 a 偺娫傪楢懕揑偵曄壔偡傞偲偒丄捈慄暘 LX 傕 A 偺忋傪楢懕揑偵 堏摦偟傑偡丅LX=0 偼 VrV'r 偵廳側傝傑偡丅
(5) LX 偺堏摦偺婳愓偼丄暯柺 A 偺忋偵俀曈偑 2a, 2b 偺暯峴巐曈宍 AX 傪宍惉偟傑偡丅 (6) Y 偺曄堟傪 -b亙Y亙b 偲偟丄曄堟撪偺侾偮偺 Y 偵懳偟偰丄挿偝 2a 偺捈慄暘 LY 傪丄捈慄暘 VrV'r 偺忋偺 Y 偵憡摉偡傞栚惙偺埵抲偵丄VrV'r 偵傛偭偰俀摍暘偝傟丄 偐偮丄HH' 偵暯峴偲側傞傛偆偵堷偒傑偡丅
(7) Y 偑 -b 偲 b 偺娫傪楢懕揑偵曄壔偡傞偲偒丄捈慄暘 LY傕A偺忋傪楢懕揑偵堏摦 偟傑偡丅LY=0 偼 HH'偵廳側傝傑偡丅
(8) LY偺堏摦偺婳愓偼丄暯柺 A 偺忋偵俀曈偑 2a, 2b 偺暯峴巐曈宍AY傪宍惉偟傑偡丅
(9) 偙偆偟偰摼偨 A 偺忋偺俀偮偺椞堟 AX偲 AY 偺嫟捠晹暘傪 AXY偲偟傑偡丅偙偺応崌丄 AX 偼 AY 偲姰慡偵廳側傞偨傔丄AXY 傕偦傟傜偲摨偠椞堟偲側傝傑偡丅 a=亣, b=亣 偺偲偒丄晛捠偵偄偆幬岎嵗昗宯偲摨偠傕偺偵側傝傑偡丅
(10) 偙偺嵗昗宯撪偺侾揰 P 偼丄偨偩侾偮偺 LX偺忋偵偁傝丄偐偮丄偨偩侾偮偺LY偺忋 偵偁傝丄偦偺嵗昗偼 (X,Y) 偲偨偩侾捠傝偵昞傢偝傟傑偡丅
(11)- (12)- (13) -a亙X亙a, -b亙Y亙b 偵偍偄偰丄俀偮偺悢偐傜側傞慻 (X,Y) 傪嶌傞偲丄偙傟傪嵗昗 偲偡傞揰 P 偑丄嵗昗宯撪偵偨偩侾偮掕傑傝傑偡丅 a=亣, b=亣 偺偲偒丄擟堄偺俀偮偺 悢偐傜側傞慻 (X,Y) 偲丄嵗昗宯撪偺侾揰 P 偲偼丄侾懳侾偵懳墳偟傑偡丅
(14) a=亣 偵偍偗傞偙偺幬岎嵗昗宯偲捈岎嵗昗宯偲偺娭學偼丄師偺捠傝偱偡丅 幬岎嵗昗傪 (X,Y)丄捈岎嵗昗傪 (W,Z) 偲偡傟偽丄
W=X+Y*Sin(r), Z=Y*Cos(r), r=幬幉偺孹幬妏(儔僕傾儞) 偲側傝傑偡丅