楕円極座標系の設定例
楕円極座標系は、極座標系の変形
の1種です。
設定の仕方によって何通りもでき
ます。
先ず、既設の極座標系を次の通り
とします。
極座標系の座標変数を X,Y 、直交
座標系の座標変数を W,Z とし、
両者の関係を
W=Y*Cos(X), 0≦X<2π
Z=Y*Sin(X), Y≧0
であるとします。
この極座標系から導かれる楕円極座標系は次のようになります。
正数 a, b をとり、
W=a*Y*Cos(X), 0≦X<2π
Z=b*Y*Sin(X), Y≧0, a>0, b>0
とすると、この X,Y が楕円極座標系を形成することとなります。
a=b=1 の場合は、普通の極座標系となります。
a≠b の場合、座標系は、普通の極座標系を上下または左右に伸縮した形となります。例えば、
a=2, b=1 の場合、楕円極座標系と直交座標系の関係は、
W=2*Y*Cos(X), 0≦X<2π
Z=Y*Sin(X), Y≧0
となります。これにより、
W2/4 +Z2=Y2
となりますから、楕円極座標系における同じ Y の値が、X の値に関係なく、直交座標系では
楕円を描くことになります。(極座標系の場合は円)
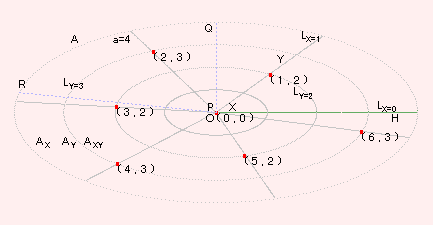
極から楕円周までの距離は、実距離が違っても、楕円極座標系においては一定です。図の点 P,Q,R
については、直交座標系としては PQ≠PR ですが、楕円極座標系で読めば、PQ=PR=4 となります。
座標系とグラフ
[色 彩]
[目で見る統計分布の姿]
先頭ページへ
