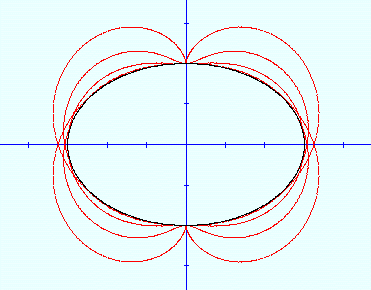
[図名] 接線関連線群６、楕円の垂足線群

[方程式] X2/A2+Y2/B2=1 （母線  楕円  黒)
         ここでは A=3, B=2

   垂足線の幾何
     初めに１つの曲線があり、これを母線とする。
     母線上に１点 Pをとり、ここに接線を引く。
     平面上に定点 Qをとり、Qから接線に下した垂
     線の足(垂足)を Rとする。
     Pと Qを定めれば、Rが定まる。
     Qを固定し、Pを動かせば、垂足 Rが動いて軌跡
     を作り、曲線となる。これを垂足線という。
     定点 Rを移動させると、垂足線群ができる。
     図では赤。 定点の座標は (0,-2), (0,-1)
     (0,1), (0,2）

   垂足線の連立方程式
     X=(T3+U2*X0+T*U*(U-Y0))/(T2+U2)
     Y=(U3+T2*Y0+T*U*(T-X0))/(T2+U2)
     T2/9+U2/4=1  T,Uは媒介変数、 (X0,Y0)は定点。

[方程式の座標系] 直交座標系

[方程式の座標変数] X,Y

[描画の座標系] 直交座標系

[描画の座標変数] X,Y

・ X:横軸、Y:縦軸、縦横等目盛、目盛の単位１

グラフィックスの目次へ   
先頭ページへ