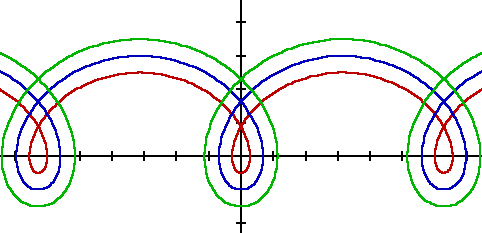
[図名] サイクロイド３

[連立方程式] X=A*(T-B*SIN(T))
             Y=A*(1-B*COS(T))

     ここでは A=1とし、Bを変化させます。

[方程式の座標系] 直交座標系

[方程式の座標変数] X,Y

[媒介変数] T

[描画の座標系] 直交座標系

[描画の座標変数] X,Y

・暗赤 A=1, B=1.5 すなわち X=T-1.5*SIN(T), Y=1-1.5*COS(T)

・濃青 A=1, B=2 すなわち X=T-2*SIN(T), Y=1-2*COS(T)

・緑 A=1, B=2.5 すなわち X=T-2.5*SIN(T), Y=1-2.5*COS(T)

・ X:横軸、Y:縦軸、縦横等目盛、目盛の単位１

サイクロイドの幾何学的説明

上記のサイクロイドは、一定直線上を円(この場合半径１)が転がるときの、
円外の点（直径の延長線上）の軌跡です。中心からの距離が Bで、図では
暗赤が B=1.5, 濃青が B=2, 緑が B=2.5となっています。

グラフィックスの目次へ   
先頭ページへ