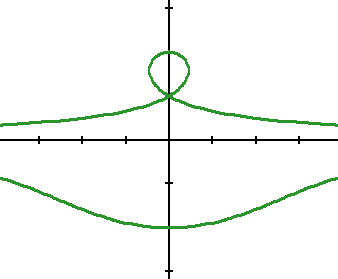
[図名] 螺獅線１

[方程式] X2*Y2=(1-Y)2*(4-Y2)

[方程式の座標系] 直交座標系

[方程式の座標変数] X,Y

[描画の座標系] 直交座標系

[描画の座標変数] X,Y

・ X:横軸、Y:縦軸、縦横等目盛、目盛の単位１

螺獅線の幾何学的説明

 定点 Aと定直線があり、Aを通る任意の直線が定直線と交わる
点を Pとし、直線 APの上に Pを端とする一定の長さの線分 PQ
を２つとります。すると、Qの軌跡が螺獅線となります。
定点 Aと定直線の距離を A，線分の長さを Bとするとき、螺獅線の方程式は、
 X2*Y2=(A-Y)2*(B2-Y2)
となります。B>Aのとき、丸い瘤ができます。上例では A=1, B=2です。
また、媒介変数で表わすと
 X=A*TAN(T)+B*SIN(T), Y=B*COS(T)
となります。

グラフィックスの目次へ   
先頭ページへ