|
Ⅰ 始めに
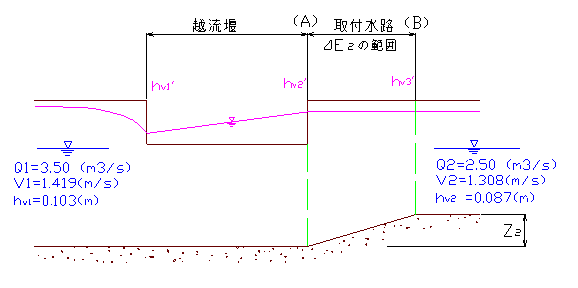
これより、計算例は漸縮による損失 fgc(hv1-hv2)は過小に、摩擦損失Im・lは過大に評価していることが分かる。また、漸縮による損失の計算で(hv1-hv2)としているが、本来この計算は(漸縮後の速度水頭-漸縮前の速度水頭)とすべきであり(p188 式(6.5.6)参照)この点でも理論的に正しくない。もっとも、ここで⊿E2を求める段階では、各地点の水深は決定されておらず、実際の水深による緒元は計算出来ないため、目的がZ2を決定するためであることからも、何らかの簡易的方法が取られる事は止む終えないが、同ペーシ下方の損失水頭の計算での He2の算式中の⊿E2はhv2'と同様He2によって決まる値であり、試算によって解けるため、これを考慮すべきである。 計算例はある特定の流況を想定して計算していいるが、実際に余水吐を設計する場合、必ずしもこのケースのような流況になるとは限らない。そこで、余水吐の目的や状況に応じての設計方法を検討するため、想定される流況についての計算結果と考察を下記に示す。なお、計算方法について上記に問題点を指摘したが、ここでの計算については、基本的に計算例に合わせて行った。 1. CASE.1-1 (計算例の場合) 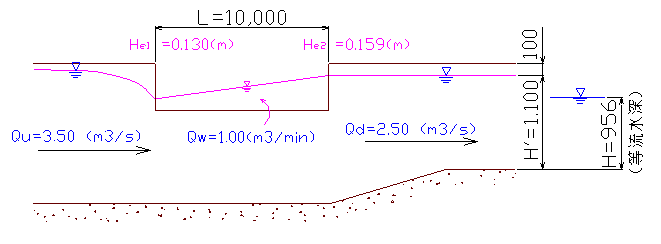 下流側の水位または流量が制御された場合の流況である。現実的には下流側に水位調整ゲートか流量を制御する施設を設けない限り、このような流況は生じない。 2. CASE.1-2 (計算例に対し、下流水位が制御されない場合) 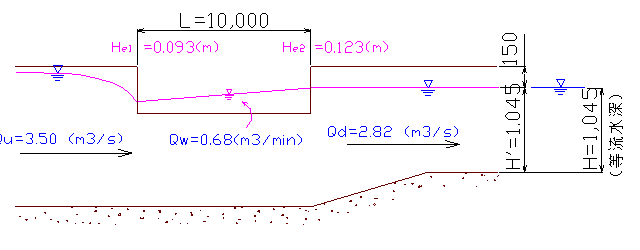 下流水位は堰やゲート等で強制的に制御されない限り、その流量に対する等流水深になるはずである。この条件の基に計算すると、上図のように下流側には設計流量Qd=2.50(m3/s)以上の流量が流れる事になる。 3. CASE.2-1 (下流水位制御で上流流量が減少した場合) 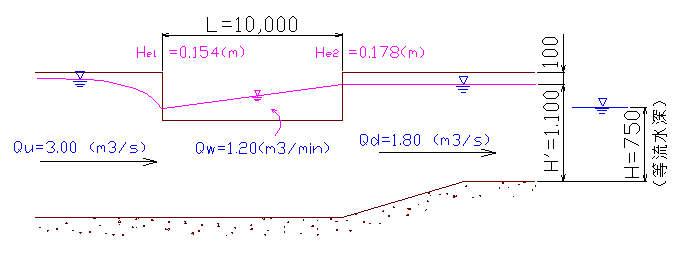 下流水位を計算例と同じH'=1.10mとし、上流流量をQu=3.50(m3/s)から3.00(m3/s)に減少させたとき、下流側流量は設計流量Qd=2.50(m3/s)より少ない1.80(m3/s)となる。これより、下流側で水位が一定に保たれている場合、上流側の流量変化に対し、下流への流量を一定に保つことが出来ないことが分かる。 4. CASE.2-2 (下流流量制御で上流流量が減少した場合)  何らかの制御施設で下流流量を制御した場合、上流側流量の変化に対し、下流側は水位変化として対応する。上流側の流量が設計流量以下であれば下流側の水位は設計水位以上に上がらないため問題ないが、水位変動に係わらず流量を一定に保つ施設が必要である。 5. CASE.2-2 (計算例の流量で下流水路の底高を上げない場合)  計算例では下流側の底高を上げているが、これを無くした場合にどうなるかを計算してみた。この場合、堰頂は下流水位以上とし堰上げ水位は水路天端-0.10m以下とするため、堰下流側の越流水深は下流水路のフリーボードに制限される。(計算例では取付水路下流端では天端-0.10mとしているが上流端では天端-0.066mとなっている)このため底を上げた場合に比べ越流水深が小さくなり、さらに速度水頭が増すため堰の長さが長くなる。 この考え方は間違っている!と思われる方は→こちらへ Ⅳ 余水吐設計への適用について 計算例で扱っている余水吐は、上流側流量が下流側流量より常に多く、それぞれに応じた水路断面が決定されている水路系をモデルとしている。現実的にこれに相当すると考えられる水路系としては ①上流からの流量の一部を放流して、必要流量のみを下流に流下させる ②洪水流入を見込んだ断面に対し、下流側は用水流量のみに対応した断面とする が考えられる。 ①の場合、Ⅲの1及び2で考察したとおり、下流流量を一定に保つためには下流水位を一定に保たなければならない。ここで、一定の上流流量に対して下流流量を一定に保つ機能は、余水吐ではなく分水施設である。(これを余水として放流するような施設は現実的でない) ②の場合、洪水時上流流量は変化するため、Ⅲの3及び4で考察したとおり特別な流量制御を行わない限り下流流量は変化する。しかし、設計で想定した流量以下であれば下流側水路が溢れることは無い。洪水流入は一時的な流れであるため、これで問題は無いが、排水路としての機能を特別多く持たせているか、地形上の制約が無い限り、底高は下流側に合わせ壁天端高を高くするほうが用水路としては一般的である。 また、余水吐を必要とする場合について考えると ③水路の余裕高の範囲内で処理できなくなった洪水等の余剰水を排除する ④河川等から取水する場合、過剰な取水量を排除する ⑤ポンプ場や分水工等、一定の流出が見込まれているものが機能しなかった場合の余水を排除する 等が考えられる。 ③は②とちがい一般の用水路の場合であり、下流水路底が上流より高くなることは殆どない。この場合、排除すべき余水は確率雨量から決定される便宜的な流量であるため、堰上下流の越流水深をそれぞれ考慮するような複雑な計算ではなく、(HWL-NWL)で決定される越流水深で堰の越流量を計算すれば良いと思われるが、それについての記述は無い ④については、河川等の水位が計画取水位より上昇した場合などが対象となる。この時、下流水路は一時的な流れとして許容される水位まで上昇させて計算してよいと考えられるが、その流量は一定に保つ事はできないため、Ⅲの2に示したような流況を考えるべきであり、計算例のようにはならない。 このような場合は、許容される下流水深に対しての流量を求め、最大取水量からこれを差し引いた流量を堰越流量として計算すべきと考える。 ⑤の場合は各々の流量は確定されるから、下流水路の水位上昇が判断条件となる。この計算は計算例のように水位を仮定しながらの試算で求めることが出来るが、取付水路に関する部分は不要である。 この考え方は間違っている!と思われる方は→こちらへ Ⅴ 終わりに 以上述べてきたように、この計算例には理論的な問題点があるばかりで無く、余水吐の事例として一般的でない。と、私は考えるのだが・・ それを言い切るだけの自信は無い。このページを見られた方の率直な意見を頂き、自己の浅学を補う材料になればと考えている。 ちなみに、この報文を書くきっかけを作ってくれたT氏であるが、前述のとおり、私の大学、コンサル、一匹狼の先輩である。コンサル時代、上司であるT氏に分からない所を聞きに行くと、質問の回答の代わりに、「これを読め」と専門書を渡されたものだ。このT氏のお陰で新米の私は随分勉強させてもらった。あれから、二十数年経った今、アプリケーションソフトに頼り、計算の詳細を熟考する事を忘れてしまった私に、再度、勉強の機会を与えてくれたT氏に感謝の意を表したい。 |