 ●桝とは 桝とは、もともと液体や穀物などの分量をはかる容器のことである。一升桝とか五合桝という一定の単位容量を持つ桝によって容量が計量されていた。相撲などの桝席という名前は、この桝に形状が似ているためと思われるが、土木の世界でも、この形から命名されたと思われる「桝」なるものが存在する。土木の世界の「桝」は、集水桝、雨水桝、汚水桝のように水路の屈曲、合流、落差部に設けられる水路構造物であり、深い桝や浅い桝、大きな桝や小さな桝と、その形は様々である。また、ポンプ場の吐水槽や畑かんの配水槽なども「桝」と呼ばれることがある。「桝」は力学的に合理的で安定した構造形式であるが、構造計算の視点で見るとなかなか奥深いものがある。 ●どう斬るか 桝構造は、本来、土圧等の荷重に対し3次元で対応する構造であるが、解析が複雑であるため、これを斬って解析しやすい2次元の構造モデルに近似する。 この時、その斬り方が問題になるが、一般的には 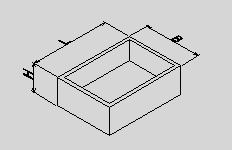 こんな桝は こんな桝は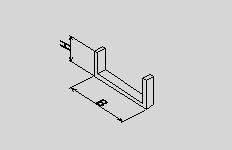 こう斬り こう斬り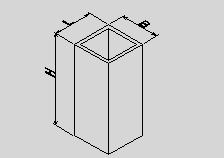 こんな桝は こんな桝は こう斬る こう斬る何故か? 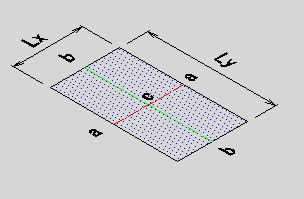 このような長方形版に等分布荷重Wがかかった場合、a-a方向及びb-b方向の梁を考えると 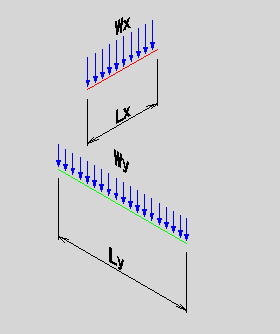 それぞれの梁の分担する荷重は、次式のように配分される, 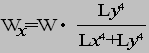 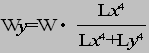 この式は、上の長方形版で、a-a方向及びb-b方向の梁を考えた場合、C点における両者のたわみは等しくなる、と言うところから導かれる(筈である)が、その意味するところは 「スパンの短い方が、より大きな荷重を分担する」と言うことである。 梁は同じ等分布荷重が作用した場合、スパンが短いほど強く、長いほど弱い。版は、強い者が弱い者を助ける、美しい助け合いの精神によって構成された構造体なのである。 このため、Ly/Lxの比がある程度大きくなれば、荷重は殆どLx方向、つまり短辺方向が受け持つため、先に挙げたような切り方で斬ったモデルで計算すれば良いことになる。 ここで、Ly/Lxがどれだけの時、短編方向のみを考えればよいかについて、コンクリート標準示方書では 「短スパンと長スパンの比が0.4以下の2方向スラブが等分布荷重を受ける場合は、荷重を短スパン方向だけで受けるものと仮定し、一方向スラブに近似して断面力を求めて良い」としている。これは、Lx/Ly≦0.4つまり Ly/Lx>2.5となる場合に短辺方向のみの計算でよいといっているが、設計基準「ポンプ場」では Ly/Lx≧2とする考え方を示しているため、農業土木においては、これに従うのが良いであろう。 Ly/Lx=2 とした時、前記の式で計算すると、版にかかる荷重の94%が短辺方向に、6%が長辺方向にかかる事になる。 ●ラーメンにする?版にする? 「ラーメンかうどんか」ならともかく、「ラーメンか版か」の問いかけは、一般の人にとって「豚とチューリップはどちらが偉いか」と聞かれるぐらい奇怪な問いかけに思えるだろう。単純なコンクリートの箱を作るのに、縦だ横だと言いながら構造計算をしていること事態、理解してもらえないかも知れない。しかし、この報文を読む人は殆ど土木の関係者だと思うので、特殊な世界の掟についての考察を続けることとする。 Ly/Lx≧2となる場合については、前述のとおりであるが、これ以外の時は、2方向スラブとして設計すべきである。しかし「ポンプ場」では 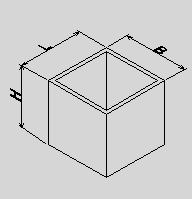 上図で 2>L/H≧1 (ただし L≧B) の時 平面ボックスラーメン か 版として計算 2>H/L≧1 (ただし L≧B) の時 フルーム か 版として計算 としている。この、どちらに付いても 「構造物の規模が大きい場合には版として解析した方が有利である」としているが、 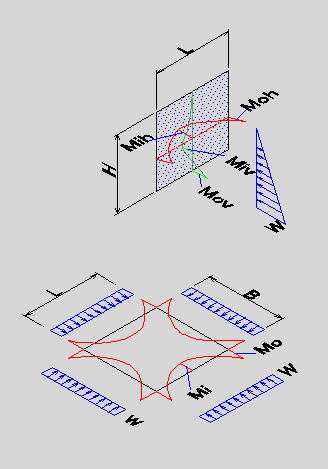 上図のように、側壁に三角形分布荷重が作用した場合に、平面ボックスラーメンとした場合と版とした場合のモメントを比較してみると 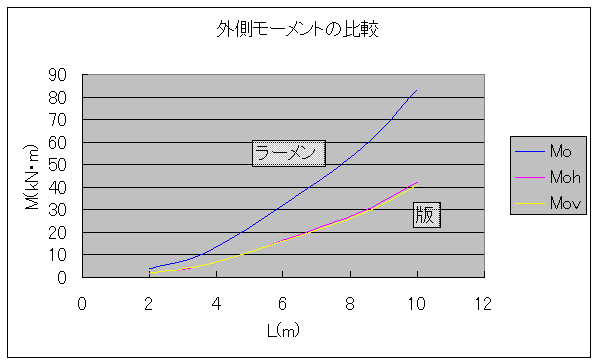 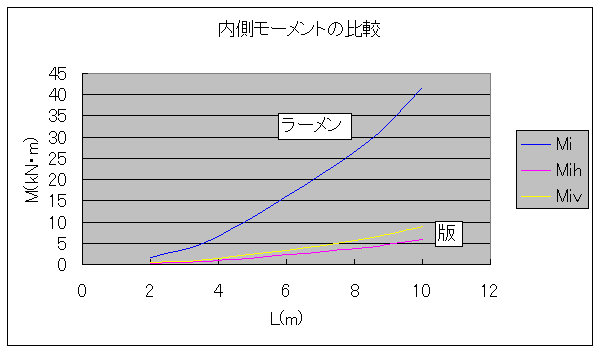 (表はW=10kN/m2 B=L H=1.5・L として計算している) 上表に見るように、モーメントの値は常にラーメンの方が大きな値を示しており、「ポンプ場」の「構造物の規模が大きい場合には・・・・」の表現は適切でない。 正しくは、「規模が小さ時は、どちらの方法で計算しても大差ないため、解析の簡単な平面ボックスラーメン(又はフルーム)として良いが、規模が大きい場合は版として計算するのが望ましい」とすべきと思われる。 版の計算は、これまで図表をつかって行うことが多く、煩雑な面があり、精度の点でも問題があったが、最近では数値解析のできる安価なソフトもあるため、これを用いれば規模の大小を意識することなく、精度のよい経済的な設計が可能である。これを考えると、いっそのこと 「このような場合は全て、版として計算する」としても良いと思われる。 しかし ●版には問題がある 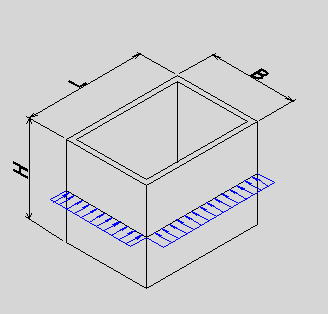 上図のような平面的に長方形の桝の側壁に等分布荷重がかかった場合を考える これを、平面ボックスラーメンで解くと、モーメントはこうなる 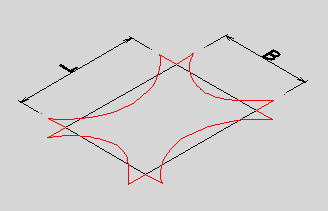 一方、側壁をそれぞれ独立した両端固定梁と考えると、こうなる 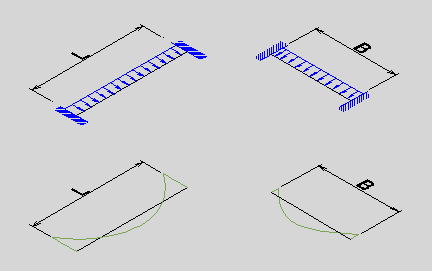 両者を重ね合わすと 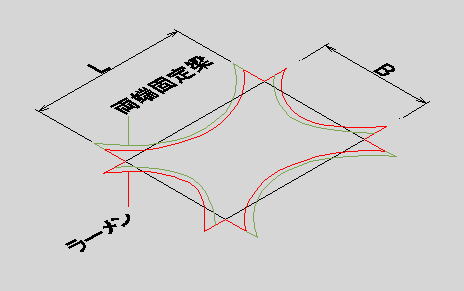 図にみるように、両端固定梁とした場合は、部材接点における長辺側と短辺側の材端モーメントが異なっている。接点位置で回転が無い限り、両者は等しくならなければならないので、実際にはこのモーメントの差分は剛比で配分される。また、部材中央のモメントも材端モーメントが変わる事によって増減する。結果としてラーメンとした場合のモーメントになるが、これが現実的なモーメントの値である。 側壁をそれぞれ独立した版として解く場合、底版及び側壁の両サイドを固定、上辺を自由とする3辺固定版として解くのが一般的である。この方法で求められた水平方向のモーメントには、両端固定梁の場合と同じ問題がある。つまり、直交する面との材端モーメントの配分を考慮していないため、長辺方向(図のL方向)では端部モーメント(外側)の値が過大に、中央部モーメント(内側)の値が過小になっている。短辺方向(図のB方向)では、その逆である。 版の計算値そのままを使って鉄筋量を決定した場合、外側の鉄筋は長辺方向の値で決定されるため、安全側であり問題ないとも言えるが、長辺方向内側の鉄筋は、必ずしも安全が保証されていない事になる。 このため、側壁を版として計算する場合は材端モーメントの配分を加味する必要があるが、そこまでするなら最初からラーメンで、と言うことで、制水弁室等、長方形桝の計算は水平ボックスラーメンで計算することが多い。 ●集水桝は桝では無い 桝で米を計っていた世代の一般人に、集水桝を指さして、「この桝が・・・」と言うと。「何でこれが桝なんだ?穴が開いてるじゃ無いか」と言われるのではないだろうか。これまで述べてきた桝は、計量容器としての桝のように、側壁が全て開口部の無い壁であることを前提としてきた、しかし、実際の集水桝には開口部があり、長辺短辺の比だけで斬り方を決められない。 たとえば  このような桝を  こう斬ったのでは計算出来ないので  こう斬るか 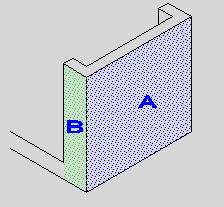 A面を版として計算することになる。この場合の版は、B面側がA面の材端モーメントを完全に拘束出来るとは考えられないため、通常の3辺固定1辺自由の版ではなく、B面に接する側を単純支持とするモデルで計算すべきである。 また、 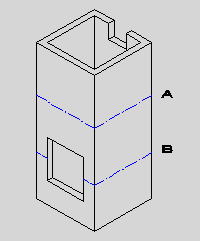 このような深い桝では、水平ボックスラーメンで計算することになるが、図のA,B面でのモーメントは 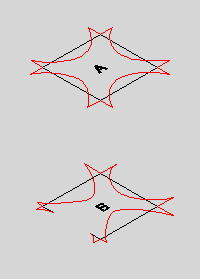 このようになり、開口部に直交する面には、一般部より大きなモーメントが発生する この部分を検討するには 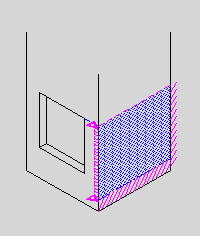 図のような、底版及び開口のない側壁側を固定、開口側を単純支持、標準部壁に荷重を負担させないため、上方を自由端とした版モデルで計算すればよい。 しかし 集水桝は通常、小規模である。こんなシビアな計算をしなくても、標準的な計算をしておけば(適当に配筋しておいても)壊れるようなことはない。 集水桝の場合、必要なのは、構造力学ではなく、構造計算書ですから〜 残念! 暇に任せてこんなこと書いてる拙者。。。。切腹〜! |