関の弟子の一人、建部彦次郎賢弘(1664-1739)が円理の発見者であったかも知れない。なぜなら、彼は優れた数学者であったし、おそらく何らかのヨーロッパの書物に精通していただろうから。とにかく、彼はこの問題について書いている。主なテーマは、正矢(versed sine)の用語で円の弧を表現することであった。建部の著作では、
は、三つの異なった無限級数によって三つの方法で正矢という言葉で表現されている。日本でその理論が更にどのように発展したかという問題は、これらの級数の起源がどこにありそうかという問題ほど面白くない。建部自身、それらの発展を理解したようには思えない。なぜなら、彼の試みた説明は、とても曖昧であるからだ。その級数は、ウォリスによって与えられてもの(2)と似ている。しかし、今まではウォリスのものと同じものとは見なされていなかった。1728年、Oyama（あるいは Awayama) Shokeiによって与えられた公式、建部によって与えられた最も一般的な公式を修正したものであるが、それでは弧の平方は、
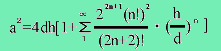のように表されるだろう。aは弧の長さ、dは直径、hは弧の高さ（正矢）である。この級数は、すでに述べたイエズス会宣教団のピエール・ジャルトゥ（Pierre Jartoux）に知られていたと言われている。それで、円理はジャルトゥの研究によって示唆されたと信ずるかなりな理由があるように思える。ジャルトゥは、ヨーロッパの資料からそれを得ていた。関派の奥義を託された人たちの中に、松永良弼（1744年没）がいた。数学的知識は、まだ一種ピタゴラスの秘儀のようにとらえられていた。彼は、その知識を師匠で関の弟子である荒木彦四郎村英（1640-1718）から受けた。松永は、日本固有の代数を大いに改良した。そして、円理法でπの値を５０桁まで計算した。
他の重要な日本の著述家の中に、三宅賢隆がいた。彼は有名な問題集（1716）ともう一つ角すい台を扱った書物を書いた。同じ頃、馬場信武（1706）は、天文学についての書を書き、球体の研究に大きな影響を与えた。
中根彦循（Genjun）（1701-1761）は、父の中根元圭（p.440）と共に、数学と天文学の研究に貢献した。それぞれ当時の中国の書物の影響を受けていたが、ヨーロッパの科学を反映したものでもあり、エイズス会宣教師たちが東洋に伝えたものであった。若い方の中根の弟子の一人が、村井中漸であった。彼は、数次係数方程式（numerical higher equation）についての書(3)を書いた（1765年）。後の著作の中で（1781年）、彼はパスカルの三角形を使って、二項式の展開における項の係数を表した。有馬頼僮（ぎょうにんべん）（1714-1783）は久留米の領主であるが、彼は関派で発達した代数理論の奥義--点竄術として知られていた理論--を最初に出版した人物であった。--これまでの習慣通り、有馬は問題の形式で提出した。これらの問題は、不定方程式、方程式の様々な根、幾何学への代数の応用、球に内接する球、最大と最小、二項級数、そして求積法に関するものであった。彼の保護下にあった中で最も優れたものは、本田定資であった。後の名、藤田貞資の名の方が知られているが。彼は代数について著名な書を書いた（1779）が(4)、他の様々な論文と共に、優れた教師であったが数学者としては何ら独創性を持っていなかったことを示している。彼と同時代の人物の中に、会田安明（1747-1817）がいた。彼は興味深い多くの級数を思いついたが、それを彼の測量術に関する著作との関連で用いた。もう一人、同時代人で、はるかに優れた数学者であった安島直円（1739-1798）は、不定方程式の理論と幾何学に貢献した者であった。彼の解決法の中に、ファルマッティ問題の代数的解法がある。また、先行者たちがしたように弧ではなく、弦を等分することで円理理論を前進させた。
１８世紀の日本の数学の最も興味深い特徴は、和算、すなわち日本固有の数学の領域に次第に西洋の理論が入り込んでいることである。日本は、問題を解くことにおいては偉大な才能を示した。しかし、決して偉大な理論に発展することはなかった。この点で独創性が最も見られるのは円理についての日本の著作の中にあった。ここでさえ、日本は、中国及びイエズス会宣教団との接触を通して始まったように思える。
１９世紀は、全国に及ぶ一般測量で始まった。その時までにはヨーロッパの資料が有効になり始めていたが、問題はまだ日本固有のものの寄せ集めであった。１８５６年にヨーロッパの方式で書かれた算術書が出版され、１８５９年には、エリアス・ルーミス（Elias Loomis）（1811-1890）による、微積分法に関するアメリカの著作が翻訳された。その時から日本の数学は新しい性格を帯びることとなった。というのは、よきにつれ悪しきにつれ、和算は死滅し、代わりにヨーロッパの学問科学が支配することになったから。日本が西洋の方法に著しい才能を発揮できるか、あるいはその逆かは、これから見ていくことになるだろう。